题型：解答题 题类：单元测试 难易度：中档
新年份：2020
如图，某市拟在长为\(8\:km\)的道路\(OP\)的一侧修建一条运动赛道，赛道的前一部分为曲线段\(OSM\)，该曲线段为函数\(y=A\sin \:ωx(A > 0 , ω > 0)\)，\(x∈[0 , 4]\)的图像，且图像的最高点为\(S(3 , 2 \sqrt{3} )\)；赛道的后一部分为折线段\(MNP\)，为保证参赛运动员的安全，限定\(∠MNP=120°\)．
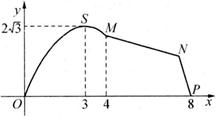
\((1)\)求\(A\)，\(ω\)的值和\(M\)，\(P\)两点间的距离；
\((2)\)应如何设计，才能使折线段赛道\(MNP\)最长\(?\)
题型：解答题 题类：单元测试 难易度：中档
新年份：2020
为了测量两山顶\(M\)，\(N\)间的距离，飞机沿水平方向在\(A\)，\(B\)两点进行测量，\(A\)，\(B\)，\(M\)，\(N\)在同一个铅垂平面内\((\)如示意图\()\)，飞机能够测量的数据有俯角和\(A\)，\(B\)间的距离，请设计一个方案，包括：①指出需要测量的数据\((\)用字母表示，并在图中标出\()\)；②用文字和公式写出计算\(M\)，\(N\)间的距离的步骤． 