题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
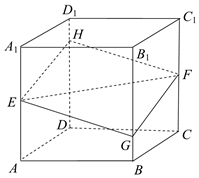 如图,正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的棱长为\(a\),\(E\),\(F\)分别是棱\(AA _{1}\),\(CC _{1}\)的中点,过点\(E\),\(F\)的平面分别与棱\(BB _{1}\),\(DD _{1}\)交于点\(G\),\(H\),设\(BG=x\),\(x∈[0 , a].\)给出以下四个命题:
如图,正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的棱长为\(a\),\(E\),\(F\)分别是棱\(AA _{1}\),\(CC _{1}\)的中点,过点\(E\),\(F\)的平面分别与棱\(BB _{1}\),\(DD _{1}\)交于点\(G\),\(H\),设\(BG=x\),\(x∈[0 , a].\)给出以下四个命题:题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020
题型:选择题 题类:月考试卷 难易度:中档
新 测年份:2020