第一章充要条件-山东版高教版（拓展上）数学同步练习题

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1819 选择本页全部试题

题型：解答题题类：月考试卷难易度：中档
新
年份：2020

如图，在四棱锥\(A-BCDE\)中，底面\(BCDE\)为矩形，侧面\(ABC⊥\)底面\(BCDE\)，\(BC=2\)，\(CD= \sqrt {2}\)，\(AB=AC\)．
\((1)\)证明：\(AD⊥CE\)；
\((2)\)设\(CE\)与平面\(ABE\)所成的角为\(45°\)，求二面角\(C-AD-E\)的余弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

如图，四棱锥\(P-ABCD\)中，侧面\(PAB\)是等腰直角三角形，\(BC⊥\)平面\(PAB\)，\(PA=PB\)，\(AB=BC=2\)，\(AD=BD= \sqrt {5}\)．
\((1)\)求证：\(PA⊥\)平面\(PBC\)：
\((2)\)求直线\(PC\)与平面\(PAD\)所成的角的正弦值．

查看解析收藏纠错相似题

+选题
题型：填空题题类：月考试卷难易度：中档
新
年份：2020

已知\(P\)为双曲线\( \dfrac {x^{2}}{a^{2}}- \dfrac {y^{2}}{b^{2}}=1(a > 0,b > 0)\)右支上一点\((\)非顶点\()\)，\(F _{1}\)、\(F _{2}\)分别为双曲线的左、右焦点，点\(M\)为\(\triangle PF _{1} F _{2}\)的内心，若\(S_{\triangle MPF_{1}}-S_{\triangle MPF_{2}}= \dfrac { \sqrt {2}}{2}S_{\triangle MF_{1}F_{2}}\)，则该双曲线的离心率为______．

查看解析收藏纠错相似题

+选题
题型：填空题题类：月考试卷难易度：中档
新
年份：2020

在三棱锥\(P-ABC\)中，\(PA⊥\)平面\(ABC\)，\(PA=AB=1\)，\(BC=2\)，\(∠BAC\geqslant \dfrac {π}{2}\)，\(M\)是线段\(BC\)上的动点，记直线\(PM\)与平面\(ABC\)所成的角为\(θ\)，若\(\tan θ\)的最大值为\( \dfrac {2 \sqrt {3}}{3}\)，\(E\)为线段\(AC\)的中点，过点\(E\)作三棱锥\(P-ABC\)外接球的截面，则该截面面积的取值范围为______．

查看解析收藏纠错相似题

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

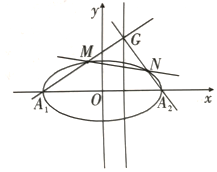已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)过点\((1, \dfrac {3}{2})\)且离心率为\( \dfrac {1}{2}\)．
\((1)\)求椭圆\(C\)的标准方程；
\((2)\)若\(A _{1}\)，\(A _{2}\)分别为\(C\)的左、右顶点，\(G\)为直线\(x=1\)上的任意一点，直线\(GA _{1}\)，\(GA _{2}\)分别与\(C\)相交于\(M\)、\(N\)两点，连接\(MN\)，试证明直线\(MN\)过定点，并求出该定点的坐标．

查看解析收藏纠错相似题

+选题
题型：选择题题类：历年真题难易度：中档
新
年份：2020

(2020•山东)已知点\( A(4，3)，B(-4，2)\)，点P在函数\( y={x}^{2}-4x-3\)图象的对称轴上，若\( \overrightarrow{PA}\perp \overrightarrow{PB}\)则点P的坐标是 (　　)

A.(2，-6)或(2.1) B.(-2，-6)或(-2，1) C.(2.6)或(2，-1) D.(-2.6)或(-2，-1)

查看解析收藏纠错相似题

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

过抛物线\(y ^{2} =2px(p > 0)\)的焦点\(F\)作抛物线的弦，与抛物线交于\(A\)，\(B\)两点，\(M\)为\(AB\)的中点，分别过\(A\)，\(B\)两点作抛物线的切线\(l _{1}\)，\(l _{2}\)相交于点\(P\)，\(\triangle PAB\)又常被称作阿基米德三角形．下面关于\(\triangle PAB\)的描述：
①\(P\)点必在抛物线的准线上；
②\(AP⊥PB\)；
③设\(A(x _{1} , y _{1} )\)，\(B(x _{2} , y _{2} )\)，则\(\triangle PAB\)的面积\(S\)的最小值为\( \dfrac {p^{2}}{2}\)；
④\(PF⊥AB\)；
⑤\(PM\)平行于\(x\)轴．
其中正确的个数是\((\:\:\:\:)\)

A.\(2\) B.\(3\) C.\(4\) D.\(5\)

查看解析收藏纠错相似题

+选题
题型：选择题题类：月考试卷难易度：中档
新测
年份：2020

已知直线\(l _{1}\)，\(l _{2}\)的方程分别为\(2mx-2y-m=0\)和\(2x+2my-3=0\)，设\(l _{1}\)，\(l _{2}\)交于点\(M\)，记点\(M\)的轨迹为曲线\(C\)，若双曲线\(C_{1}： \dfrac {x^{2}}{a^{2}}- \dfrac {y^{2}}{b^{2}}=1(a > 0,b > 0)\)的渐近线与曲线\(C\)没有公共点，则双曲线\(C _{1}\)的离心率的取值范围是\((\:\:\:\:)\)

A.\((1, \dfrac { \sqrt {6}}{2})\) B.\(( \sqrt {6},+∞)\) C.\((1, \dfrac {4 \sqrt {2}}{3})\) D.\(( \dfrac {2 \sqrt {3}}{3},+∞)\)

查看解析收藏纠错相似题

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

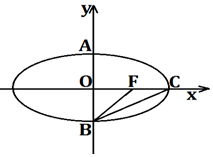如图所示，已知椭圆\(E\)的离心率为\( \dfrac { \sqrt {2}}{2}\)，\(A\)，\(B\)，\(C\)，\(F\)分别为椭圆的上顶点、下顶点、右顶点和右焦点，且\(\triangle BCF\)的面积为\(2 \sqrt {2}-2\)．
\((1)\)求椭圆\(E\)的方程；
\((2)\)是否存在过点\(B\)的直线\(l\)，使得\(l\)与椭圆\(E\)交于另一点\(D\)，且\(\triangle ABD\)是以\(BD\)为底边的等腰三角形，若存在，请求出此时直线\(l\)的方程，若不存在，请说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：中档
新
年份：2020

已知直三棱柱\(A _{1} B _{1} C _{1} -ABC\)中，\(AB=AC=AA _{1} =1\)，\(∠BAC=90°\)．
\((1)\)求异面直线\(A _{1} B\)与\(B _{1} C _{1}\)所成角；
\((2)\)求点\(B _{1}\)到平面\(A _{1} BC\)的距离．

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心