题型：选择题 题类：其他 难易度：中档
测年份：2018
\(\alpha{,}\beta\)是两个不同的平面，\(m\mathrm{{ }}{,}n\)是两条不同的直线，有下列四个命题：
\(①\)如果\(m{⊥}n\mathrm{{ }}{,}m{⊥}\alpha{,}n{/\!/}\beta\) ，那么\(\alpha{⊥}\beta\)；
\(②\)如果\(m{⊥}\alpha{,}m{⊥}\beta\)，那么\(\alpha{/\!/}\beta\)；
\(③\)如果\(\alpha{/\!/}\beta\)，\(m{⊂}\alpha\)，那么\(m{/\!/}\beta\)；
\(④\)如果\(\alpha\)内有不共线的三个点到\(\beta\)的距离相等，那么\(\alpha{/\!/}\beta.\)其中正确命题的序号为( )
题型：选择题 题类：月考试卷 难易度：中档
测年份：2018
设\(m\)，\(n\)是两条不同的直线，\(\alpha\)，\(\beta\)是两个不同的平面，则正确的结论是\((\) \()\)
题型：选择题 题类：其他 难易度：中档
测年份：2018
平面\(a\)过正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)的顶点\(A\)，\(a/\!/\)平面\(CB_{1}D_{1}\)，\(a∩ \)平面\(ABCD=m\)，\(a∩ \)平面\(ABA_{1}B_{1}=n\)，则\(m\)，\(n\)所成角的正弦值为\((\) \()\)
题型：选择题 题类：其他 难易度：中档
测年份：2018
在直三棱柱\((\)侧棱垂直于底面的棱柱\()ABC-A_{1}B_{1}C_{1}\)中，平面\(α\)与棱\(AB\)，\(AC\)，\(A_{1}C_{1}\)，\(A_{1}B_{1}\)分别交于点\(E\)，\(F\)，\(G\)，\(H\)，且直线\(AA_{1}/\!/\)平面\(α.\)有下列三个命题：\(①\)四边形\(EFGH\)是平行四边形；\(②\)平面\(α/\!/\)平面\(BCC_{1}B_{1}\)；\(③\)平面\(α⊥\)平面\(BCFE.\)其中正确的命题有
题型：选择题 题类：其他 难易度：中档
测年份：2018
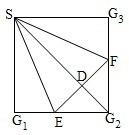在正方形\(SG_{1}G_{2}G_{3}\)中，\(E\)、\(F\)分别是\(G_{1}G_{2}\)及\(G_{2}G_{3}\)的中点，\(D\)是\(EF\)的中点，现在沿\(SE\)、\(SF\)及\(EF\)把这个正方形折成一个四面体，使\(G_{1}\)、\(G_{2}\)、\(G_{3}\)三点重合，重合后的点记为\(G\)，那么，在四面体\(S-EFG\)中必有\((\) \()\) 题型：选择题 题类：其他 难易度：中档
测年份：2018
如图，已知一个八面体的各条棱长均为\(1\)，四边形\(ABCD\)为正方形，给出下列命题：
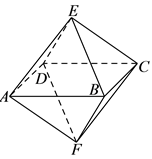
\(①\)不平行的两条棱所在的直线所成的角是\(60{}^\circ \)或\(90{}^\circ \)；
\(②\)四边形\(AECF\)是正方形；
\(③\)点\(A\)到平面\(BCE\)的距离为\(1\)；
\(④\)平面\(ADE\)与平面\(BCE\)所成的锐二面角的余弦值为\(\dfrac{1}{2}\)．
其中正确的命题有\((\) \()\)．
