题型：解答题 题类：期末考试 难易度：较易
新年份：2021
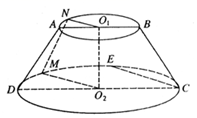已知圆台\(O_{1}O_{2}\)，轴截面\(ABCD\)，圆台的上底面圆半径与高相等，下底面圆半径为高的两倍，点\(E\)为下底圆弧\(\overparen{CD}\)的中点，点\(N\)为上底圆周上靠近点\(A\)的\(\overparen{AB}\)的四等分点，经过\(O_{1}\)，\(O_{2}\)，\(N\)三点的平面与弧\(\overparen{CD}\)交于点\(M\)，且\(E\)，\(M\)，\(N\)三点在平面\(ABCD\)的同侧.
如图，在圆柱\(OO_{1}\)中，\(AB\)是圆柱的母线，\(BC\)是圆柱的底面\(⊙O\)的直径，\(D\)是底面圆周上异于\(B\)、\(C\)的点．
如图，在三棱锥\(P-ABC\)中，\(E\)，\(F\)分别是\(PA\)，\(AB\)的中点，\(G\)，\(H\)分别是\(PC\)，\(BC\)上的点，且\(\dfrac{CG}{GP}=\dfrac{CH}{HB}=\dfrac{1}{2}.\)
如图，四边形\(ABCD\)是直角梯形，\(AB/\!/CD\)，\(AB=AD=1\)，\(CD=2\)，\(AB⊥AD\)，\(PC⊥\)平面\(ABCD\)，\(E\)为\(PC\)的中点．