题型:解答题 题类:其他 难易度:难
年份:2018
如图,在三棱柱\(ABC-A_{1}B_{1}C_{1}\)中,\(∠B_{1}A_{1}A=∠C_{1}A_{1}A=60^{\circ}\),\(AA_{1}=AC=4\),\(AB=2\),\(P\),\(Q\)分别为棱\(AA_{1}\),\(AC\)的中点.
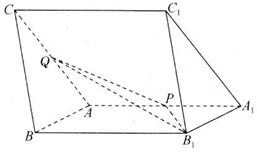
\((1)\)在平面\(ABC\)内过点\(A\)作\(AM/\!/\)平面\(PQB_{1}\)交\(BC\)于点\(M\),并写出作图步骤,不要求证明;
\((2)\)若侧面\(ACC_{1}A_{1}⊥\)侧面\(ABB_{1}A_{1}\),求直线\(A_{1}C_{1}\)与平面\(PQB_{1}\)所成角的正弦值.
题型:解答题 题类:其他 难易度:难
年份:2018
如图,在四棱锥\(P-ABCD\)中,底面\(ABCD\)是菱形,且\(\angle ABC=120{}^\circ \),点\(E\)是棱\(PC\)的中点,平面\(ABE\)与棱\(PD\)交于点\(F\).

\((1)\)求证:\(AB\parallel EF\).
\((2)\)若\(PA=PD=AD=2\),且平面\(PAD\bot \)平面\(ABCD\),求:
\(①\)二面角\(E-AF-D\)的锐二面角的余弦值.
\(②\)在线段\(PC\)上是否存在一点\(H\),使得直线\(BH\)与平面\(AEF\)所成角等于\(60{}^\circ \),若存在,确定\(H\)的位置,若不存在,说明理由.