题型：解答题 题类：期末考试 难易度：中档
新年份：2020
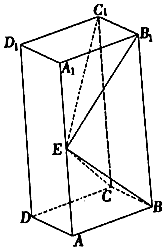如图，长方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的底面\(ABCD\)是正方形，点\(E\)在棱\(AA _{1}\)上，\(B _{1} E⊥EC\)．题型：选择题 题类：期末考试 难易度：中档
新 测年份：2020
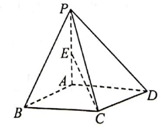在\(《\)九章算术\(》\)中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”\(.\)如图，四棱锥\(P-ABCD\)为阳马，侧棱\(PA⊥\)底面\(ABCD\)，\(PA=AB=AD\)，\(E\)为棱\(PA\)的中点，则直线\(CE\)与平面\(PAD\)所成角的正弦值为\((\:\:\:\:)\) 题型：解答题 题类：期末考试 难易度：中档
新年份：2020
题型：解答题 题类：期末考试 难易度：中档
新年份：2020
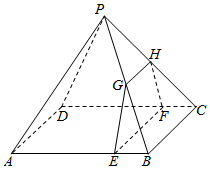如图，四棱锥\(P-ABCD\)的底面是边长为\(4\)的正方形，四条侧棱长均为\( \sqrt {17} .\)点\(G\)，\(E\)，\(F\)，\(H\)分别是棱\(PB\)，\(AB\)，\(CD\)，\(PC\)上共面的四点，平面\(GEFH⊥\)平面\(ABCD\)，\(BC/\!/\)平面\(GEFH\)．
如图，若正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的棱长为\(1\)，则异面直线\(AC\)与\(A _{1} B\)所成的角的大小是______；直线\(A _{1} B\)和底面\(ABCD\)所成的角的大小是______． 
如图，在棱长为\(2\)的正方体中\(ABCD-A _{1} B _{1} C _{1} D _{1}\)，点\(M\)是\(AD\)的中点，动点\(P\)在底面\(ABCD\)内\((\)包括边界\()\)，若\(B _{1} P/\!/\)平面\(A _{1} BM\)，则\(C _{1} P\)与底面\(ABCD\)所成角的正切值的取值范围是______． 
如图，在四棱锥\(P-ABCD\)中，\(PA=PB= \sqrt {2}\)，底面\(ABCD\)为边长为\(2\)的菱形，且\(∠BAD= \dfrac {π}{3}\)．
在四棱锥\(P-ABCD\)中，\(PA⊥\)平面\(ABCD\)，\(BC/\!/AD\)，\(∠CDA=90°\)，\(AD=2BC=2\)，\(CD= \sqrt {2}\)，\(PM=2MC\)．
已知矩形\(ABCD\)中，\(AD=2AB=2\)，\(E\)，\(F\)分別为\(AD\)，\(BC\)的中点，现将矩形\(ABCD\)沿\(EF\)折起，使二面角\(D{'}-EF-B\)为\(60°\)．