代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1258选择本页全部试题

题型：解答题题类：模拟题难易度：较难
新
年份：2020

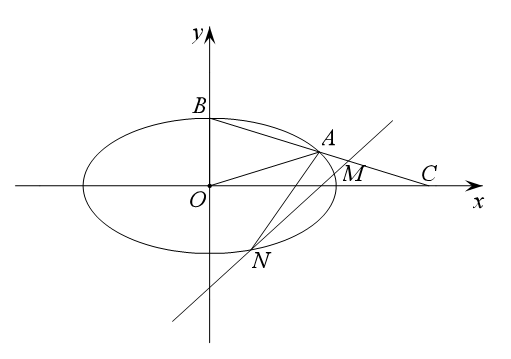如图所示，在平面直角坐标系\(xOy\)中，已知椭圆\(E\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1 (a > b > 0)\)的离心率为\( \dfrac { \sqrt {3}}{2}\)，\(A\)为椭圆\(E\)上位于第一象限上的点，\(B\)为椭圆\(E\)的上顶点，直线\(AB\)与\(x\)轴相交于点\(C\)，\(|AB|=|AO|\)，\(\triangle BOC\)的面积为\( \sqrt {3}\)．
\((1)\)求椭圆\(E\)的标准方程；
\((2)\)设直线\(l\)过椭圆\(E\)的右焦点，且与椭圆\(E\)相交于\(M\)，\(N\)两点\((M , N\)在直线\(OA\)的同侧\()\)，若\(∠CAM=∠OAN\)，求直线\(l\)的方程．

查看解析收藏纠错

+选题
题型：选择题题类：模拟题难易度：较难
新测
年份：2020

已知函数\(f(x)\)满足：①对任意\(0\leqslant x _{1} < x _{2}\)，都有\( \dfrac {f(x_{1})-f(x_{2})}{x_{1}-x_{2}} < 0\)；②函数\(y=f(x+2)\)的图象关于点\((-2 , 0)\)对称．若实数\(a\)，\(b\)满足\(f(a ^{2} +2b)\leqslant -f(-b ^{2} -2a)\)，则当\(a∈[ \dfrac {1}{2},1]\)时，\( \dfrac {a}{a+b}\)的取值范围为\((\:\:\:\:)\)

A.\([ \dfrac {1}{8}, \dfrac {1}{2}]\) B.\([ \dfrac {1}{4}, \dfrac {1}{2}]\) C.\([ \dfrac {1}{2},1]\) D.\([2 , 4]\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知抛物线\(C\)：\(x ^{2} =2py(p > 0)\)的焦点为\(F\)，点\(Q\)在抛物线\(C\)上，点\(P\)的坐标为\((1, \dfrac {1}{2})\)，且满足\( \overrightarrow {OF}+2 \overrightarrow {FP}= \overrightarrow {FQ} (O\)为坐标原点\()\)．
\((1)\)求抛物线\(C\)的方程；
\((2)\)若直线\(l\)交抛物线\(C\)于\(A\)，\(B\)两点，且弦\(AB\)的中点\(M\)在直线\(y=2\)上，试求\(\triangle OAB\)的面积的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知椭圆\(C： \dfrac {x^{2}}{a^{2}}+y^{2}=1(a > 1)\)的左、右焦点分别为\(F _{1}\)，\(F _{2}\)，过点\(F _{1}\)的直线\(l\)的倾斜角为锐角，\(P\)为椭圆的上顶点，且\(PF _{1} ⊥PF _{2}\)．
\((\)Ⅰ\()\)求椭圆\(C\)的方程；
\((\)Ⅱ\()\)若直线\(l\)与椭圆\(C\)交异于点\(P\)的两点\(A\)，\(B\)，且直线\(PA\)，\(PB\)与直线\(x+y-2=0\)分别交于不同两点\(M\)、\(N\)，当\(|MN|\)最小时，求直线\(l\)的方程．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)的左、右焦点分别为\(F _{1}\)，\(F _{2}\)，椭圆\(C\)短轴两顶点和两焦点构成的四边形为正方形，且周长为\(4 \sqrt {2}\)，经过\(F _{2}\)与坐标轴不垂直的直线\(l\)交椭圆于\(M\)，\(N\)两点．
\((1)\)求椭圆\(C\)的标准方程；
\((2)\)若椭圆\(C\)短轴上的点\(T(0 , t)\)，满足\(|TM|=|TN|\)，求实数\(t\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知椭圆\(M： \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)的一个焦点与短轴的两端点组成一个正三角形的三个顶点，且椭圆经过点\(N( \sqrt {2}, \dfrac { \sqrt {2}}{2})\)．
\((1)\)求椭圆\(M\)的方程；
\((2)\)若斜率为\(- \dfrac {1}{2}\)的直线\(l _{1}\)与椭圆\(M\)交于\(P\)，\(Q\)两点\((\)点\(P\)，\(Q\)不在坐标轴上\()\)；证明：直线\(OP\)，\(PQ\)，\(OQ\)的斜率依次成等比数列．
\((3)\)设直线\(l _{2}\)与椭圆\(M\)交于\(A\)，\(B\)两点，且以线段\(AB\)为直径的圆过椭圆的右顶点\(C\)，求\(ABC\)面积的最大值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知椭圆\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)的右焦点为\(F\)，\(T\)为椭圆上一点，\(O\)为坐标原点，椭圆的离心率为\( \dfrac { \sqrt {2}}{2}\)，且\(\triangle TFO\)面积的最大值为\( \dfrac {1}{2}\)．
\((1)\)求椭圆的方程；
\((2)\)设点\(A(0 , 1)\)，直线\(l\)：\(y=kx+t(t\neq ±1)\)与椭圆\(C\)交于两个不同点\(P\)，\(Q\)，直线\(AP\)与\(x\)轴交于点\(M\)，直线\(AQ\)与\(x\)轴交于点\(N\)，若\(|OM|\boldsymbol{⋅}|ON|=2\)，求证：直线\(l\)经过定点．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

在三棱柱\(ABC-A _{1} B _{1} C _{1}\)中，侧面\(AA _{1} C _{1} C⊥\)底面\(ABC\)，\(AA _{1} =A _{1} C=AC=AB=BC=2\)，且点\(O\)为\(AC\)中点．
\((1)\)证明：\(A _{1} O⊥BC\)；
\((2)\)求三棱锥\(C _{1} -ABC\)的体积．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

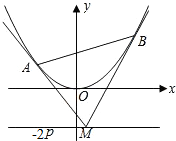如图，设抛物线方程为\(x ^{2} =2py(p > 0)\)，\(M\)为直线\(y=-2p\)上任意一点，过\(M\)引抛物线的切线，切点分别为\(A\)，\(B\)．
\((\)Ⅰ\()\)设线段\(AB\)的中点为\(N\)；
\((ⅰ)\)求证：\(MN\)平行于\(y\)轴；
\((ⅱ)\)已知当\(M\)点的坐标为\((2 , -2p)\)时，\(|AB|=4 \sqrt {10}\)，求此时抛物线的方程；
\((\)Ⅱ\()\)是否存在点\(M\)，使得点\(C\)关于直线\(AB\)的对称点\(D\)在抛物线\(x ^{2} =2py(p > 0)\)上，其中，点\(C\)满足\( \overrightarrow {OC}= \overrightarrow {OA}+ \overrightarrow {OB} (O\)为坐标原点\().\)若存在，求出所有适合题意的点\(M\)的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

\((1)\)填空：\(C _{ n-1 }^{ m } +C _{ n+1 }^{ m+1 } =C _{ m }^{ n }\)及\( \dfrac {m}{n} C _{ n }^{ m } =C _{ y }^{ m+1 } (n\geqslant 2 , n∈N* , m∈N*).\)则\(x=\)______\(y=\)______\((\)结果用\(m\)，\(n\)表示\()\)
\((2)\)已知\(f(n)= \dfrac {1}{2} C _{ n }^{ 0 } - \dfrac {1}{3} C _{ n }^{ 1 } + \dfrac {1}{4} C _{ n }^{ 2 } +……+(-1) ^{n} \dfrac {1}{n+2} C _{ n }^{ n }\)，\(n∈N*.\)猜想\(f(n)\)的表达式并用数学归纳法证明你的结论．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心