题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
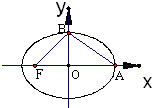 如图,椭圆中心在坐标原点,\(F\)为左焦点,当\( \overrightarrow {FB}⊥ \overrightarrow {AB}\)时,其离心率为\( \dfrac { \sqrt {5}-1}{2}\),此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为\((\:\:\:\:)\)
如图,椭圆中心在坐标原点,\(F\)为左焦点,当\( \overrightarrow {FB}⊥ \overrightarrow {AB}\)时,其离心率为\( \dfrac { \sqrt {5}-1}{2}\),此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为\((\:\:\:\:)\) 题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020
题型:选择题 题类:期中考试 难易度:较难
新 测年份:2020