职教组卷基于海量职教高考试题库建立的在线组卷及学习系统

网站首页帮助中心注册

职教组卷

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：155选择本页全部试题

题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆C：=1（a＞b＞0）．
（1）若椭圆的离心率为，且点（1，）在椭圆上，
①求椭圆的方程；
②设P（-1，-），R、S分别为椭圆C的右顶点和上顶点，直线PR和PS与y轴和x轴相交于点M，N，求直线MN的方程．
（2）设D（b，0），过D点的直线l与椭圆C交于E、F两点，且E、F均在y轴的右侧，=2，求椭圆离心率的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆C：的短轴长为2，离心率为．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）直线l平行于直线y=x，且与椭圆C交于A，B两个不同的点，若∠AOB为钝角，求直线l在x轴上的截距m的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD=CD=1，∠ADC=120°，PA=AB=BC=，点M是AC与BD的交点．
（1）求二面角A-PC-B的余弦值；
（2）若点N在线段PB上且MN∥平面PDC，求直线MN与平面PAC所成角的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

2020元旦联欢晚会上，A，B两班各设计了一个摸球表演节目的游戏：A班在一个纸盒中装有1个红球，1个黄球，1个白球，这些球除颜色外完全相同，记事件A_n：同学们有放回地每次摸出1个球，重复n次，n次摸球中既有红球，也有黄球，还有白球；B班在一个纸盒中装有1个蓝球，1个黑球，这些球除颜色外完全相同，记事件B_n：同学们有放回地每次摸出1个球，重复n次，n次摸球中既有蓝球，也有黑球，事件A_n发生的概率为P（A_n），事件B_n发生的概率为P（B_n）．
（1）求概率P（A₃），P（A₄）及P（B₃），P（B₄）；
（2）已知P（A_n）=aP（A_n-1）+b^n-1P（B_n-1），其中a，b为常数，求P（A_n）．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD为正三角形，M是PC的中点，过M的平面α平行于平面PAB，且平面α与平面PAD的交线为ON，与平面ABCD的交线为OE．
（1）在图中作出四边形MNOE（不必说出作法和理由）；
（2）若，求平面α与平面PBC形成的锐二面角的余弦值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

近年来，国家为了鼓励高校毕业生自主创业，出台了许多优惠政策，以创业带动就业．某高校毕业生小张自主创业从事苹果的种植，并开设网店进行销售．为了做好苹果的品控，小张从自己果园的苹果树上，随机摘取150个苹果测重（单位：克），其重量分布在区间[100，400]内，根据统计的数据得到如图1所示的频率分布直方图．

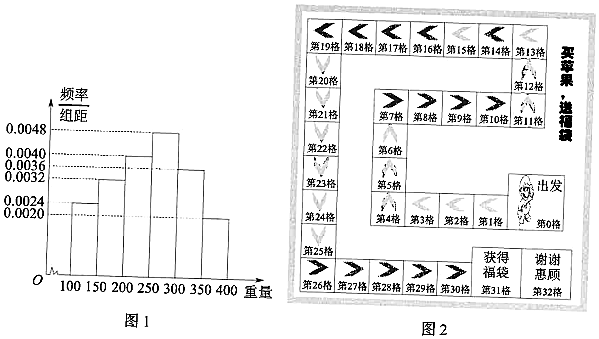
（1）以上述样本数据中频率作为概率，现一顾客从该果园购买了30个苹果，求这30个苹果中重量在（300，400]内的个数X的数学期望；
（2）小张的网店为了进行苹果的促销，推出了“买苹果，送福袋”的活动，买家在线参加按图行进赢取福袋的游戏该游戏的规则如下：买家点击抛掷一枚特殊的骰子，每次抛掷的结果为1或2，且这两种结果的概率相同；从出发格（第0格）开始，每掷一次，按照抛掷的结果，按如图2所示的路径向前行进一次，若掷出1点，即从当前位置向前行进一格（从第k格到第k+1格，k∈N，若掷出2点，即从当前位置向前行进两格（从第k格到第k+2格，k∈N）行进至第31格（获得福袋）或第32格（谢谢惠顾），游戏结束．设买家行进至第i格的概率为p_i，（i=0，1，2，…，32），p₀=1．
（i）求p₁、p₂，并写出用p_i-2、p_i-1表示p_i（i=2，3，…，31）的递推式；
（ii）求P₃₂，并说明该大学生网店推出的此款游戏活动，是更有利于卖家，还是更有利于买家．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知函数．
（1）当a=1时
①求函数f（x）在（2，f（2））处的切线方程；
②定义其中n∈N*，求S₂₀₂₀；
（2）当a≠2时，设t（x）=f（x）-ln（4x-x²），g（x）=xe^1-x（e为自然对数的底数），若对任意给定的x₀∈（0，e]，在（0，e]上总存在两个不同的x_i（i=1，2），使得t（x_i）=g（x₀）成立，求a的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆C:的离心率为，A，B分别为C的左右顶点.
（1）求C的方程；
（2）若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BPBQ,求APQ的面积.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知椭圆（a＞b＞0）的离心率为，短轴的一个端点到右焦点的距离为2．
（1）试求椭圆M的方程；
（2）设圆O：x²+y²=r²（r＞0）是椭圆M长轴和短轴四个端点连接而成的四边形的内切圆，过圆O上的任一点A作圆O的切线交椭圆M于B，C两点，求证：|AB||AC|=r²．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难
新
年份：2020

已知等差数列{a_n}和等比数列{b_n}的各项均为整数，它们的前n项和分别为S_n，T_n，且b₁=2a₁=2，b₂S₃=54，a₂+T₂=11．
（1）求数列{a_n}，{b_n}的通项公式；
（2）求M_n=a₁b₁+a₂b₂+a₃b₃+…+a_nb_n；
（3）是否存在正整数m，使得恰好是数列{a_n}或{b_n}中的项？若存在，求出所有满足条件的m的值；若不存在，说明理由．

查看解析收藏纠错

+选题

服务介绍

帮助中心

微信服务号

联系电话

18165375674