代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1605选择本页全部试题

题型：解答题题类：历年真题难易度：中档
新
年份：2022

(2022•山东)(本小题7分)已知函数\( \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{k}}{\mathrm{x}}\),且\( \mathrm{f}\left(2\right)=1\).
(1)求实数k的值;
(2)证明函数\( \left(\mathrm{x}\right)\)在\( (0,+\mathrm{\infty })\)上是减函数

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2022

(2022•山东)(本小题8分)如图所示,在正方体\( \mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}-{\mathrm{A}}_{1}{\mathrm{B}}_{1}{\mathrm{C}}_{1}{\mathrm{D}}_{1}\)中,P是棱\( {\mathrm{B}}_{1}\mathrm{B}\)上的点,求证:

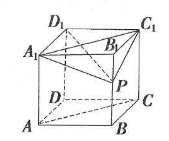
(1)\( \mathrm{A}\mathrm{C}//\)平面\( {\mathrm{A}}_{1}\mathrm{P}{\mathrm{C}}_{1}\);
(2)\( \mathrm{A}\mathrm{C}\perp {\mathrm{D}}_{1}\mathrm{P}\)

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2022

(2022•山东)(本小题8分)已知函数\( \mathrm{f}\left(\mathrm{x}\right)=2\sqrt{3}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}-2\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\mathrm{x}+\mathrm{m}\)的图象过点\( (0,-1)\)
(1)求函数\( f\left(\mathrm{x}\right)\)的最大值;
(2)若\( \mathrm{\alpha }\in (0,\frac{\mathrm{\pi }}{2})\),且\( \mathrm{f}\left(\mathrm{\alpha }\right)=1\).求\( \mathrm{\alpha }\)的值.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

已知四棱锥P-ABCD中，侧面PAD⊥底面ABCD，∠BAD=60°，△PAD是边长为2的正三角形，底面ABCD是菱形，点M为PC的中点．
（1）求证：PA∥平面MDB；
（2）求三棱锥A-BDM的体积．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

在△ABC中，三内角A，B，C满足．
（Ⅰ）判断△ABC的形状；
（Ⅱ）若点D在线段AC上，且CD=2DA，，求tanA的值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

如图所示，在平面直角坐标系xOy中，已知椭圆E：=1（a＞b＞0）的离心率为，A为椭圆E上位于第一象限上的点，B为椭圆E的上顶点，直线AB与x轴相交于点C，|AB|=|AO|，△BOC的面积为6．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）设直线l过椭圆E的右焦点，且与椭圆E相交于M，N两点（M，N在直线OA的同侧），若∠CAM=∠OAN，求直线l的方程

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

(2020•山东)某男子擅长走路，9天共走了1260里，其中第1天，第4天，第7天所走的路程之和为390里.若从第2天起，每天比前一天多走的路程相同，问该男子第5天走多少里.这是我国古代数学专著《九章算术》中的一个问题，请尝试解决.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

(2020•山东)小明同学用"五点法"作某个正弦型函数\( y=Asin(\omega x＋\phi )(A>0,\omega >0,|\phi |<\frac{\pi }{2})\)一个周期内的图象时，列表如下:

根据表中数据，求:
(1)实数\( A.\omega ·\phi \)的值;
(2)该函数在区间\( \left[\frac{3\pi }{4},\frac{5\pi }{4}\right]\)上的最大值和最小值.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

在四棱锥P-ABCD中，底面ABCD为直角梯形，BC∥AD，∠ADC=90°，BC=CD=AD=1，E为线段AD的中点，PE⊥底面ABCD，点F是棱PC的中点，平面BEF与棱PD相交于点G．
（Ⅰ）求证：BE∥FG；
（Ⅱ）若PC与AB所成的角为，求直线PB与平面BEF所成角的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2020

已知椭圆w：（a＞b＞0）过A（0，1），B（0，-1）两点，离心率为．
（Ⅰ）求椭圆w的方程；
（Ⅱ）过点A的直线l与椭圆w的另一个交点为C，直线l交直线y=2于点M，记直线BC，BM的斜率分别为k₁，k₂，求k₁k₂的值．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心