代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：1294选择本页全部试题

题型：解答题题类：月考试卷难易度：较易
新
年份：2020

某小区超市采取有力措施保障居民正常生活的物资供应．为做好日常生活必需的甲类物资的供应，超市对社区居民户每天对甲类物资的购买量进行了调查，得到了以下频率分布直方图\((\)如图\()\)．

\((\)Ⅰ\()\)估计该小区居民对甲类物资购买量的中位数；
\((\)Ⅱ\()\)现将小区居民按照购买量分为两组，即购买量在\([1 , 3)\)单位：\(kg)\)的居民为\(A\)组，购买量在\([3 , 6](\)单位：\(kg]\)的居民为\(B\)组，采用分层抽样的方式从该小区中选出\(5\)户进行生活情况调查，再从这\(5\)户中随机选出\(3\)户，求选出的\(B\)组户数为\(2\)的概率．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

如图，在四棱锥\(A-BCDE\)中，底面\(BCDE\)为矩形，侧面\(ABC⊥\)底面\(BCDE\)，\(BC=2\)，\(CD= \sqrt {2}\)，\(AB=AC\)．
\((1)\)证明：\(AD⊥CE\)；
\((2)\)设\(CE\)与平面\(ABE\)所成的角为\(45°\)，求二面角\(C-AD-E\)的余弦值．

查看解析收藏纠错

+选题

题型：解答题题类：月考试卷难易度：较易

新

年份：2020

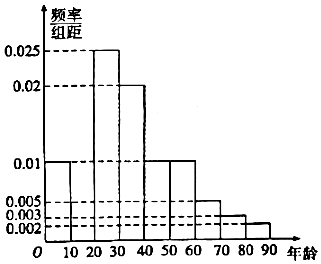汉中黎坪景区位于陕西省汉中市南郑区黎坪镇境内，国家\(AAA\)级旅游景区，东西长\(18\)公里，南北宽\(13\)公里，总面积约\(94.3\)平方千米，是以森林景观、地貌景观、水体景观以及现代入文景观和田园风光景观为主，集山景、林景、水景、石景、气候景观和田园景观为一体的山岳型旅游景区．某学校社团为了解游客的具体情形以及采集旅客对景区的建议，特别在\(2020\)年\(6\)月\(1\)日旅游旺季对进园游客进行取样调查，从当日\(12000\)名游客中抽取\(100\)人进行统计分析，结果如下：

年龄	频数	频率	男	女
\([0 , 10)\)	\(10\)	\(0.1\)	\(5\)	\(5\)
\([10 , 20)\)	①	②	③	④
\([20 , 30)\)	\(25\)	\(0.25\)	\(12\)	\(13\)
\([30 , 40)\)	\(20\)	\(0.2\)	\(10\)	\(10\)
\([40 , 50)\)	\(10\)	\(0.1\)	\(6\)	\(4\)
\([50 , 60)\)	\(10\)	\(0.1\)	\(3\)	\(7\)
\([60 , 70)\)	\(5\)	\(0.05\)	\(1\)	\(4\)
\([70 , 80)\)	\(3\)	\(0.03\)	\(1\)	\(2\)
\([80 , 90)\)	\(2\)	\(0.02\)	\(0\)	\(2\)
合计	\(100\)	\(1.00\)	\(45\)	\(55\)

\((1)\)完成表一中的空位①\(～\)④，并在答题纸中补全频率分布直方图，并估计\(2020\)年\(6\)月\(1\)日当日接待游客中\(30\)岁以下的游客人数；
\((2)\)完成表二，并判断能否有\(97.5\%\)的把握认为在游客中“年龄达到\(50\)岁以上\((\)含\(50\)岁\()\)”与“性别相关；
\((3)\)按分层抽样\((\)分\(50\)岁以上\((\)含\(50\)岁\()\)与\(50\)岁以下两层\()\)抽取被调查的\(100\)位游客中的\(10\)人作为幸运游客免费领取黎坪内部景区门票，再从这\(10\)人中选取\(2\)人接受电视台采访，设这\(2\)人中年龄在\(50\)岁以上\((\)含\(50\)岁\()\)的人数为\(ξ\)，求\(ξ\)的分布列．

	\(50\)岁以上	\(50\)岁以下	合计
男生
女生
合计

\(P(K ^{2} \geqslant k)\)	\(0.15\)	\(0.10\)	\(0.05\)	\(0.025\)	\(0.010\)	\(0.005\)	\(0.001\)
\(k\)	\(2.072\)	\(2.706\)	\(3.841\)	\(5.024\)	\(6.635\)	\(7.879\)	\(10.828\)

\((\)参考公式：\(K ^{2} = \dfrac {n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}\)，其中\(n=a+b+c+d.)\)

查看解析收藏纠错

+选题

题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知数列\(\{a _{n} \}\)的前\(n\)项和为\(S _{n}\)，且\(S _{n} =2a _{n} -n(n∈N*)\)．
\((1)\)求\(a _{1}\)，\(a _{2}\)，\(a _{3}\)，的值，猜想数列\(\{a _{n} \}\)的通项公式并加以证明；
\((2)\)求\(a _{1} +a _{3} +a _{5} +…+a _{2n+3} (n∈N*)\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知数列\(\{a _{n} \}\)的前\(n\)项和\(S _{n}\)满足\(S _{n} = \dfrac {n^{2}+5n}{2}\)，\(n∈N*\)．
\((1)\)求数列\(\{a _{n} \}\)的通项公式；
\((2)\)设\(b _{n} =2 ^{a_{n}} +(-1) ^{n} a _{n}\)，\(n∈N*\)，求数列\(\{b _{n} \}\)的前\(2n\)项和\(T _{2n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较难
新
年份：2020

设等差数列\(\{a _{n} \}\)的前\(n\)项和为\(S _{n}\)，且\(5S _{5} =S _{10}\)，\(a _{4} =2a _{6} +20\)．
\((1)\)求数列\(\{a _{n} \}\)的通项公式；
\((2)\)若数列\(\{b _{n} \}\)满足\( \dfrac {b_{1}}{a_{1}} + \dfrac {b_{2}}{a_{2}} +…+ \dfrac {b_{n}}{a_{n}} = \dfrac {1}{2^{n}} -1\)，\(n∈N*\)，证明：\(b _{n} \leqslant \dfrac {5}{8}\)．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

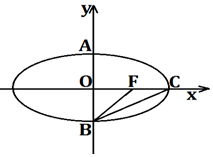如图所示，已知椭圆\(E\)的离心率为\( \dfrac { \sqrt {2}}{2}\)，\(A\)，\(B\)，\(C\)，\(F\)分别为椭圆的上顶点、下顶点、右顶点和右焦点，且\(\triangle BCF\)的面积为\(2 \sqrt {2}-2\)．
\((1)\)求椭圆\(E\)的方程；
\((2)\)是否存在过点\(B\)的直线\(l\)，使得\(l\)与椭圆\(E\)交于另一点\(D\)，且\(\triangle ABD\)是以\(BD\)为底边的等腰三角形，若存在，请求出此时直线\(l\)的方程，若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知函数\(g(x)=x ^{2} -2x+a\)在\(x∈[1 , m]\)时有最大值为\(1\)，最小值为\(0\)．
\((1)\)求实数\(a\)的值；
\((2)\)设\(f(x)= \dfrac {g(x)}{x}\)，若不等式\(f(2 ^{x} )-k\boldsymbol{⋅}2 ^{x} \leqslant 0\)在\(x∈[0 , 1]\)上恒成立，求实数\(k\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知定义在\(R\)上的函数\(f(x)= \dfrac {b-2^{x}}{2^{x+1}+a} (a∈R , b∈R)\)是奇函数．
\((1)\)求\(a\)，\(b\)的值；
\((2)\)当\(x∈(1 , 2)\)时，不等式\(2 ^{x} +kf(x)-3 > 0\)恒成立，求实数\(k\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：中档
新
年份：2020

已知数列\(\{a _{n} \}\)满足\(a_{1}= \dfrac {3}{2}\)，且\(a _{n+1} =λa _{n} +1(n∈N* , λ∈R\)且\(λ\neq - \dfrac {2}{3} ).\)
\((1)λ\)为何值时，数列\(\{a _{n} +1\}\)是等比数列；
\((2)\)若数列\(\{a _{n} +1\}\)是等比数列，求数列\(\{a _{n} \}\)的前\(n\)项和\(S _{n}\)．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心