题型:解答题 题类:模拟题 难易度:较难
新年份:2020
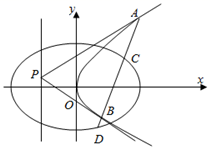 已知点\(P\)是抛物线\(C _{1}\):\(y ^{2} =4x\)的准线上任意一点,过点\(P\)作抛物线\(C _{1}\)的两条切线\(PA\),\(PB\),其中\(A\),\(B\)为切点.
已知点\(P\)是抛物线\(C _{1}\):\(y ^{2} =4x\)的准线上任意一点,过点\(P\)作抛物线\(C _{1}\)的两条切线\(PA\),\(PB\),其中\(A\),\(B\)为切点.题型:解答题 题类:月考试卷 难易度:较难
新年份:2020
题型:解答题 题类:月考试卷 难易度:较难
新年份:2020
题型:解答题 题类:模拟题 难易度:较难
新年份:2020
题型:解答题 题类:模拟题 难易度:较难
新年份:2020
题型:解答题 题类:模拟题 难易度:较难
新年份:2020
题型:解答题 题类:月考试卷 难易度:较难
新年份:2020
题型:解答题 题类:期中考试 难易度:较难
新年份:2020
题型:解答题 题类:月考试卷 难易度:较难
新年份:2020