代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：623选择本页全部试题

题型：解答题题类：期中考试难易度：较难
新
年份：2020

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c\)，已知\(B= \dfrac {π}{4}\)，\(\cos A+\cos 2A=0\)．
\((1)\)求角\(C\)；
\((2)\)若\(b ^{2} +c ^{2} =a+bc+2\)，求\(\triangle ABC\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

如图所示，在直三棱柱\(ABCA _{1} B _{1} C _{1}\)中，\(E\)，\(F\)分别为\(A _{1} C _{1}\)和\(BC\)的中点．
\((1)\)求证：\(EF/\!/\)平面\(AA _{1} B _{1} B\)；
\((2)\)若\(AA _{1} =3\)，\(AB=2 \sqrt {3}\)，求\(EF\)与平面\(ABC\)所成的角．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

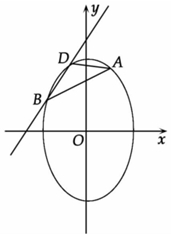已知点\(A(1, \sqrt {2})\)是椭圆\(C： \dfrac {y^{2}}{a^{2}}+ \dfrac {x^{2}}{b^{2}}=1(a > b > 0)\)上的一点，椭圆\(C\)的离心率与双曲线\(x ^{2} -y ^{2} =1\)的离心率互为倒数，斜率为\( \sqrt {2}\)直线\(l\)交椭圆\(C\)于\(B\)，\(D\)两点，且\(A\)，\(B\)，\(D\)三点互不重合．
\((1)\)求椭圆\(C\)的方程；
\((2)\)若\(k _{1}\)，\(k _{2}\)分别为直线\(AB\)，\(AD\)的斜率，求证：\(k _{1} +k _{2}\)为定值．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

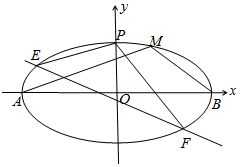已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)的左焦点\(F(- \sqrt {3},0)\)，椭圆的两顶点分别为\(A(-a , 0)\)，\(B(a , 0)\)，\(M\)为椭圆上除\(A\)，\(B\)之外的任意一点，直线\(MA\)，\(BM\)的斜率之积为\(- \dfrac {1}{4}\)．
\((\)Ⅰ\()\)求椭圆\(C\)的标准方程；
\((\)Ⅱ\()\)若\(P\)为椭圆\(C\)短轴的上顶点，斜率为\(k\)的直线\(l\)不经过\(P\)点且与椭圆\(C\)交于\(E\)，\(F\)两点，设直线\(PE\)，\(PF\)的斜率分别为\(k _{1}\)，\(k _{2}\)，且\(k _{1} +k _{2} =-1\)，试问直线\(l\)是否过定点，若是，求出这定点；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

如图，在四棱锥\(O-ABCD\)中，底面\(ABCD\)是边长为\(1\)的菱形，\(∠ABC= \dfrac {π}{3}\)，\(OA⊥\)底面\(ABCD\)，\(OA=2\)，\(M\)为\(OA\)的中点，\(N\)为\(BC\)的中点．
\((1)\)证明：直线\(MN/\!/\)平面\(OCD\)；
\((2)\)求异面直线\(AB\)与\(MD\)所成角的余弦值．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

已知抛物线\(C _{1}\)：\(y ^{2} =2px(p > 0)\)，圆\(C _{2}\)：\((x-4) ^{2} +y ^{2} =4.\)抛物线\(C _{1}\)的焦点到其准线的距离恰好是圆\(C _{2}\)的半径．
\((1)\)求抛物线\(C _{1}\)的方程及其焦点坐标；
\((2)\)过抛物线\(C _{1}\)上一点\(Q(\)除原点外\()\)作抛物线\(C _{1}\)的切线，交\(y\)轴于点\(P.\)过点\(Q\)作圆\(C _{2}\)的两条切线，切点分别为\(M\)、\(N.\)若\(MN/\!/PQ\)，求\(\triangle PMN\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

已知椭圆方程为\( \dfrac {x^{2}}{6}+ \dfrac {y^{2}}{3}=1\)．
\((1)\)设椭圆的左右焦点分别为\(F _{1}\)、\(F _{2}\)，点\(P\)在椭圆上运动，求\( \overrightarrow {PF_{1}}\cdot \overrightarrow {PF_{2}}\)的取值范围；
\((2)\)设直线\(l\)和圆\(x ^{2} +y ^{2} =2\)相切，和椭圆交于\(A\)、\(B\)两点，\(O\)为原点，线段\(OA\)、\(OB\)分别和圆\(x ^{2} +y ^{2} =2\)交于\(C\)、\(D\)两点，设\(ΔAOB\)、\(ΔCOD\)的面积分别为\(S _{1}\)、\(S _{2}\)，求\( \dfrac {S_{1}}{S_{2}}\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

已知等差数列\(\{a _{n} \}\)的首项\(a _{1} =1\)，公差\(d=1\)，前\(n\)项和为\(S _{n}\)，\(b_{n}= \dfrac {1}{S_{n}}\)，
\((1)\)求数列\(\{b _{n} \}\)的通项公式；
\((2)\)求证：\(b _{1} +b _{2} +…+b _{n} < 2\)．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

设\(D\)是函数\(y=f(x)\)定义域的一个子集，若存在\(x _{0} ∈D\)，使得\(f(x _{0} )=-x _{0}\)成立，则称\(x _{0}\)是\(f(x)\)的一个“准不动点”，也称\(f(x)\)在区间\(D\)上存在准不动点．已知\(f(x)=\log _{ \frac {1}{2}}(4^{x}+a\cdot 2^{x}-1),x∈[0,1]\)．
\((1)\)若\(a=1\)，求函数\(f(x)\)的准不动点；
\((2)\)若函数\(f(x)\)在区间\([0 , 1]\)上存在准不动点，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

已知函数\(f(x)=ax ^{2} +bx+c\)．
\((1)\)当\(a=1\)，\(b=2\)时，若存在\(x _{1}\)，\(x _{2} ∈[-2 , 0](x _{1} \neq x _{2} )\)，使得\(|f(x _{i} )|=2(i=1 , 2)\)，求实数\(c\)的取值范围；
\((2)\)若二次函数\(y=f(x)\)对一切\(x∈R\)恒有\(x ^{2} -2x+4\leqslant f(x)\leqslant 2x ^{2} -4x+5\)成立，且\(f(5)=27\)，求\(f(11)\)的值；
\((3)\)是否存在一个二次函数\(f(x)\)，使得对任意正整数\(k\)，当\(x= \overset{}{k\text{个}5}\)时，都有\(f(x)= \overset{}{2k\text{个}5}\)成立，请给出结论，并加以证明．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心