代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：331选择本页全部试题

题型：选择题题类：模拟题难易度：较难
新测
年份：2020

在正四面体\(D-ABC(\)所有棱长均相等的三棱锥\()\)中，点\(E\)在棱\(AB\)上，满足\(AE=2EB\)，点\(F\)为线段\(AC\)上的动点\(.\)设直线\(DE\)与平面\(DBF\)所成的角为\(α\)，则\((\:\:\:\:)\)

A.存在某个位置，使得\(DE⊥BF\) B.存在某个位置，使得\(∠FDB= \dfrac {π}{4}\) C.存在某个位置，使得平面\(DEF⊥\)平面\(DAC\) D.存在某个位置，使得\(α= \dfrac {π}{6}\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

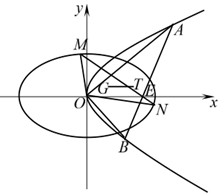如图所示，在直角坐标系\(xOy\)中，\(A\)，\(B\)是抛物线\(C_{1}：y^{2}=2px(p > 0)\)上两点，\(M\)，\(N\)是椭圆\(C_{2}： \dfrac {x^{2}}{6}+ \dfrac {y^{2}}{3}=1\)两点，若\(AB\)与\(MN\)相交于点\(E(2 , 0)\)，\( \overrightarrow {OA}\cdot \overrightarrow {OB}=-p^{2}\)．
\((\)Ⅰ\()\)求实数\(p\)的值及抛物线\(C\)，的准线方程．
\((\)Ⅱ\()\)设\(\triangle OMN\)的面积为\(S\)，\(\triangle OMN\)、\(\triangle OAB\)的重心分别为\(G\)，\(T\)，当\(GT\)平行于\(x\)轴时，求\(|GT|+S ^{2}\)的最大值．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：较难
新
年份：2020

定义数列\(\{a _{n} \}\)，先给出\(a _{1} =1\)，接着复制该项，再添加\(1\)的后继数\(2\)，于是\(a _{2} =1\)，\(a _{3} =2\)，接下来再复制前面所有项，之后再添加\(2\)的后继数\(3\)，如此继续\((1 , 1 , 2 , 1 , 1 , 2 , 3 , 1 , 1 , 2 , 1 , 1…)\)，设\(S _{n}\)是\(a _{n}\)的前\(n\)项和，则\(S _{2020} =\)______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

今有一个“数列过滤器”，它会将进入的无穷非减正整数数列删去某些项，并将剩下的项按原来的位置排好形成一个新的无穷非减正整数数列，每次“过滤”会删去数列中除以\(M\)余数为\(N\)的项，将这样的操作记为\(L(M , N)\)操作．设数列\(\{a _{n} \}\)是无穷非减正整数数列．
\((1)\)若\(a _{n} =2 ^{n-1}\)，\(n∈N ^{+}\)，\(\{a _{n} \}\)进行\(L(2 , 1)\)操作后得到\(\{b _{n} \}\)，设\(a _{n} +b _{n}\)前\(n\)项和为\(S _{n}\)
①求\(S _{n}\)．
②是否存在\(p\)，\(q\)，\(r∈N ^{+}\)，使得\(S _{p}\)，\(S _{q}\)，\(S _{r}\)成等差？若存在，求出所有的\((p , q , r)\)；若不存在，说明理由．
\((2)\)若\(a _{n} =n\)，\(n∈N ^{+}\)，对\(\{a _{n} \}\)进行\(L(4 , 0)\)与\(L(4 , 1)\)操作得到\(\{b _{n} \}\)，再将\(\{b _{n} \}\)中下标除以\(4\)余数为\(0\)，\(1\)的项删掉最终得到\(\{c _{n} \}\)证明：每个大于\(1\)的奇平方数都是\(\{c _{n} \}\) 中相邻两项的和．

查看解析收藏纠错

+选题
题型：选择题题类：模拟题难易度：较难
新测
年份：2020

已知函数\(f(x)=2\sin (ωx+φ)+h\)的最小正周期为\(π\)，若\(|f(x)|\)在\([0, \dfrac {π}{4}]\)上的最大值为\(M\)，则\(M\)的最小值为\((\:\:\:\:)\)

A.\(2 \sqrt {2}\) B.\( \sqrt {2}\) C.\(1\) D.\( \dfrac {2- \sqrt {2}}{2}\)

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

设集合\(T _{n} =\{1 , 2 , 3 , … , n\}(\)其中\(n\geqslant 3\)，\(n∈N ^{*} )\)，将\(T _{n}\)的所有\(3\)元子集\((\)含有\(3\)个元素的子集\()\)中的最小元素的和记为\(S _{n}\)．
\((1)\)求\(S _{3}\)，\(S _{4}\)，\(S _{5}\)的值；
\((2)\)试求\(S _{n}\)的表达式．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

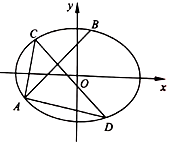如图，在平面直角坐标系\(xOy\)中，椭圆\(E\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1 (a > b > 0)\)过点\((1 , \dfrac { \sqrt {2}}{2} )\)，且椭圆的离心率为\( \dfrac { \sqrt {2}}{2}\)，直线\(l\)：\(y=x+t\)与椭圆\(E\)相交于\(A\)、\(B\)两点，线段\(AB\)的中垂线交椭圆\(E\)于\(C\)、\(D\)两点．
\((1)\)求椭圆\(E\)的标准方程；
\((2)\)求线段\(CD\)长的最大值；
\((3)\)求\( \overrightarrow {AC}\cdot \overrightarrow {AD}\)的值．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：较难
新
年份：2020

已知正四棱锥\(P-ABCD\)的底面边长为\(4 \sqrt {6}\)，高为\(6 \sqrt {2}\)，其内切球与面\(PAB\)切于点\(M\)，球面上与\(P\)距离最近的点记为\(N\)，若平面\(α\)过点\(M\)，\(N\)且与\(AB\)平行，则平面\(α\)截该正四棱锥所得截面的面积为______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

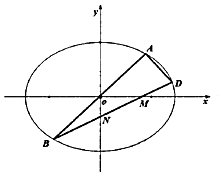如图，已知椭圆\(C： \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1\)经过\((2 , 0)\)和\((0, \sqrt {2})\)，过原点的一条直线\(l\)交椭圆于\(A\)，\(B\)两点\((A\)在第一象限\()\)，椭圆\(C\)上点\(D\)满足\(AD⊥AB\)，连直线\(BD\)与\(x\)轴、\(y\)轴分别交于\(M\)、\(N\)两点，\(\triangle ABD\)的重心在直线\(x= \dfrac {13}{21}\)的左侧．
\((1)\)求椭圆的标准方程；
\((2)\)记\(\triangle AOM\)、\(\triangle OMN\)面积分别为\(S _{1}\)、\(S _{2}\)，求\(S _{1} -S _{2}\)的取值范围．

查看解析收藏纠错

+选题
题型：选择题题类：模拟题难易度：较难
新测
年份：2020

已知数列\(\{a _{n} \}\)由首项\(a _{1} =a\)及递推关系\(a_{n+1}= \dfrac {3a_{n}-1}{a_{n}+1}\)确定．若\(\{a _{n} \}\)为有穷数列，则称\(a\)为“坏数”\(.\)将所有“坏数”从小到大排成数列\(\{a _{n} \}\)，若\(b _{2019} < a _{1} < b _{2020}\)，则\((\:\:\:\:)\)

A.\(-1 < a _{2020} < 0\) B.\(0 < a_{2020} < \dfrac {1}{3}\) C.\(a _{2020} > 3\) D.\(1 < a _{2021} < 3\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心