题型：解答题 题类：其他 难易度：中档
年份：2018
底面为菱形的直棱柱\(ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)中，\(E\)，\(F\)分别为棱\({A}_{1}{B}_{1},{A}_{1}{D}_{1} \)的中点．
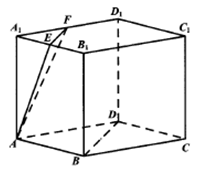
\((\)Ⅰ\()\)在图中作一个平面\(\alpha \)，使得\(BD\subset \alpha \)，且平面\(AEF/\!/\alpha .(\)不必给出证明过程，只要求作出\(\alpha \)与直棱柱\(ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)的截面\()\)．
\((\)Ⅱ\()\)若\(AB=A{{A}_{1}}=2,\angle BAD={{60}^{0}}\)，求点\(C\)到所作截面\(\alpha \)的距离．
如图，已知四棱锥\(P-ABCD\)，底面\(ABCD\)为菱形，\(PA⊥\)平面\(ABCD\)，\(∠ABC=60^{\circ}\)，\(E\)，\(F\)分别是\(BC\)，\(PC\)的中点．
在几何体\(ABCDE\)中，\(∠BAC= \dfrac {π}{2}\)，\(DC⊥\)平面\(ABC\)，\(EB⊥\)平面\(ABC\)，\(F\)是\(BC\)的中点，\(AB=AC=BE=2\)，\(CD=1\) 
如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．
