选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1258选择本页全部试题

题型：解答题题类：期末考试难易度：较难
新
年份：2020

设数列\(\left\{ {{a}_{n}} \right\}\)的前\(n\)项和为\({{S}_{n}}\)，已知\({{a}_{1}}=1\)，\({{S}_{n+1}}-2{{S}_{n}}=1\)，\(n\in {{N}^{*}}\)．
\((1)\)证明：\(\left\{ {{S}_{n}}+1 \right\}\)为等比数列，求出\(\left\{ {{a}_{n}} \right\}\)的通项公式\(;\)
\((2)\)若\({{b}_{n}}=\dfrac{n}{{{a}_{n}}}\)，求\(\left\{ {{b}_{n}} \right\}\)的前\(n\)项和\({{T}_{n}}\)，并判断是否存在正整数\(n\)使得\({{T}_{n}}\cdot {{2}^{n-1}}=n+50\)成立\(?\)若存在求出所有\(n\)值\(;\)若不存在说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：月考试卷难易度：较难
新
年份：2020

学生考试中答对但得不了满分的原因多为答题不规范，具体表现为：解题结果正确，无明显推理错误，但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等，记此类解答为“\(B\)类解答“\(.\)为评估此类解答导致的失分情况，某市教研室做了一项试验：从某次考试的数学试卷中随机抽取若干属于“\(B\)类解答“的题目，扫描后由近百名数学老师集体评阅，统计发现，满分\(12\)分的题，阅卷老师所评分数及各分数所占比例大约如表：

教师评分\((\)满分\(12\)分\()\) \(11\) \(10\) \(9\)

各分数所占比例 \( \dfrac {1}{4}\) \( \dfrac {1}{2}\) \( \dfrac {1}{4}\)

某次数学考试试卷评阅采用“双评\(+\)仲裁”的方式，规则如下：两名老师独立评分，称为一评和二评，当两者所评分数之差的绝对值小于等于\(1\)分时，取两者平均分为该题得分；当两者所评分数之差的绝对值大于\(1\)分时，再由第三位老师评分，称之为仲裁，取仲裁分数和一、二评中与之接近的分数的平均分为该题得分；当一、二评分数和仲裁分数差值的绝对值相同时，取仲裁分数和前两评中较高的分数的平均分为该题得分．\((\)假设本次考试阅卷老师对满分为\(12\)分的题目中的“\(B\)类解答”所评分数及比例均如上表所示，比例视为概率，且一、二评与仲裁三位老师评分互不影响\()\)．
\((1)\)本次数学考试中甲同学某题\((\)满分\(12\)分\()\)的解答属于“\(B\)类解答”，求甲同学此题得分\(X\)的分布列及数学期望\(E(X)\)；
\((2)\)本次数学考试有\(6\)个解答题，每题满分均为\(12\)分，同学乙\(6\)个题的解答均为“\(B\)类解答”，记该同学\((6\)个题中得分为\(x _{i} (x _{1} < x _{2} < x _{3} < x _{4} < x _{5} )\)的题目个数为\(a _{i}\)，\(a _{i} ∈N(i=1 , 2 , 3 , 4 , 5)\)，\( \sum\limits_{i=1}^{5}a_{i}=6 .\)，计算事件“\(a _{1} +a _{4} +a _{5} =4\)”的概率．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知\(\{a _{n} \}\)是各项均为正数的无穷数列，且满足\(a _{1} =a\)，\(a _{n+1} -a _{n} = \sqrt {d(a_{n+1}+a_{n})}\)．
\((1)\)若\(d=1\)，\(a _{3} =6\)，求\(a\)的值；
\((2)\)设数列\(\{b _{n} \}\)满足\(b _{n} =a _{n+1} -a _{n}\)，其前\(n\)项的和为\(S _{n}\)．
①求证：\(\{b _{n} \}\)是等差数列；
②若对于任意的\(n∈N ^{*}\)，都存在\(m∈N ^{*}\)，使得\(S _{n} =b _{m}\)成立．求证：\(S _{n} \leqslant (2 ^{n} -1)b _{1}\)．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：较难
新
年份：2020

任意实数\(a\)，\(b\)，定义\(a⊕b= \begin{cases} {ab,ab\geqslant 0} \\ { \dfrac {a}{b},ab < 0}\end{cases}\)，设函数\(f(x)=\ln x⊕x\)，正项数列\(\{a _{n} \}\)是公比大于\(0\)的等比数列，且\(a _{1010} =1\)，\(f(a _{1} )+f(a _{2} )+f(a _{3} )+…+f(a _{2019} )+f(a _{2020} )=-e\)，则\(a _{2020} =\)______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知直四棱柱\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的棱长均相等，且\(∠BAD=60°\)，\(M\)是侧棱\(DD _{1}\)的中点，\(N\)是棱\(C _{1} D _{1}\)上的点．
\((1)\)求异面直线\(BD _{1}\)与\(AM\)所成角的余弦值；
\((2)\)若二面角\(M-AC-N\)的大小为\( \dfrac {π}{4}\)，试确定点\(N\)的位置．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：较难
新
年份：2020

已知函数\(f(x)=ax ^{2} +bx+c\)．
\((1)\)当\(a=1\)，\(b=2\)时，若存在\(x _{1}\)，\(x _{2} ∈[-2 , 0](x _{1} \neq x _{2} )\)，使得\(|f(x _{i} )|=2(i=1 , 2)\)，求实数\(c\)的取值范围；
\((2)\)若二次函数\(y=f(x)\)对一切\(x∈R\)恒有\(x ^{2} -2x+4\leqslant f(x)\leqslant 2x ^{2} -4x+5\)成立，且\(f(5)=27\)，求\(f(11)\)的值；
\((3)\)是否存在一个二次函数\(f(x)\)，使得对任意正整数\(k\)，当\(x= \overset{}{k\text{个}5}\)时，都有\(f(x)= \overset{}{2k\text{个}5}\)成立，请给出结论，并加以证明．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知正项数列\(\{a _{n} \}\)的前\(n\)项和为\(S _{n}\)，且满足\(8S _{n} =16a _{n} ^{2} +n-1\)，数列\(\{b _{n} \}\)满足\(b _{n} = \sqrt {2}b_{n-1} (n\geqslant 2)\)，\(b _{1} = \dfrac { \sqrt {2}}{2}\)．
\((\)Ⅰ\()\)求数列\(\{a _{n} \}\)、\(\{b _{n} \}\)的通项公式；
\((\)Ⅱ\()\)记数列\(\{c _{n} \}\)满足\(c _{n} =[(-1) ^{n-1} +1]a _{n} +[(-1) ^{n} +1]b _{n}\)，设数列\(\{ \dfrac {c_{2n-1}}{c_{2n}}\}\)的前\(n\)项和为\(A _{n}\)，数列\(\{ \dfrac {2}{c_{2n-1}C_{2n+1}}\}\)的前\(n\)项和为\(B _{n}\)，试比较\(A _{n}\)与\(B _{n}\)的大小．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

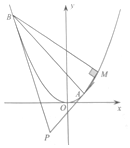已知抛物线\(C\)的方程为\(x ^{2} =2y\)，\(A\)，\(B\)为抛物线上两点，且\(MA⊥MB\)，其中\(M(2 , 2)\)，过\(A\)，\(B\)分别作抛物线\(C\)的切线\(l _{1}\)，\(l _{2}\)，设\(l _{1}\)，\(l _{2}\)交于点\(P\)．
\((I)\)如果点\(P\)的坐标为\((-2 , 0)\)，求弦长\(|AB|\)；
\((\)Ⅱ\()O\)为坐标原点，设抛物线\(C\)的焦点为\(F\)，求\( \dfrac {|OP|^{2}}{|AF|+|BF|}\)的取值范围．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：较难
新
年份：2020

已知数列\(\{a _{n} \}\)满足：对任意\(n∈N*\)，\(a _{n} ∈(0 , \dfrac {π}{2} )\)，且\(a _{1} = \dfrac {π}{3}\)，\(f(a _{n+1} )= \sqrt {f{'}(a_{n})}\)，其中\(f(x)=\tan x\)，则使得\(\sin a _{1} ×\sin a _{2} ×…×\sin a _{k} < \dfrac {1}{10}\)成立的最小正整数\(k\)为______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较难
新
年份：2020

已知\(A(1 , 2)\)为抛物线\(y ^{2} =2px(p > 0)\)上的一点，\(E\)，\(F\)为抛物线上异于点\(A\)的两点，且直线\(AE\)的斜率与直线\(AF\)的斜率互为相反数．
\((1)\)求直线\(EF\)的斜率；
\((2)\)设直线\(l\)过点\(M(m , 0)\)并交抛物线于\(P\)，\(Q\)两点，且\( \overrightarrow {PM} = λ \overrightarrow {MQ} (λ > 0)\)，直线\(x=-m\)与\(x\)轴交于点\(N\)，试探究\( \overrightarrow {MN}\)与\( \overrightarrow {NP} - λ \overrightarrow {NQ}\)的夹角是否为定值，若是则求出定值，若不是，说明理由．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心

教师评分\((\)满分\(12\)分\()\)	\(11\)	\(10\)	\(9\)
各分数所占比例	\( \dfrac {1}{4}\)	\( \dfrac {1}{2}\)	\( \dfrac {1}{4}\)