对于各项均为整数的数列{a
n},如果满足a
i+i(i=1,2,3,…)为完全平方数,则称数列{a
n}具有“P性质”;
不论数列{a
n}是否具有“P性质”,如果存在与{a
n}不是同一数列的{b
n},且{b
n}同时满足下面两个条件:①b
1,b
2,b
3,…,b
n是a
1,a
2,a
3,…,a
n的一个排列;②数列{b
n}具有“P性质”,则称数列{a
n}具有“变换P性质”.
(Ⅰ)设数列{a
n}的前n项和
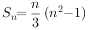
,证明数列{a
n}具有“P性质”;
(Ⅱ)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换P性质”,具有此性质的数列请写出相应的数列{b
n},不具此性质的说明理由;
(Ⅲ)对于有限项数列A:1,2,3,…,n,某人已经验证当n∈[12,m
2](m≥5)时,数列A具有“变换P性质”,试证明:当n∈[m
2+1,(m+1)
2]时,数列A也具有“变换P性质”.
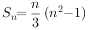 ,证明数列{an}具有“P性质”;
,证明数列{an}具有“P性质”;