题型：解答题 题类：月考试卷 难易度：较易
新年份：2021
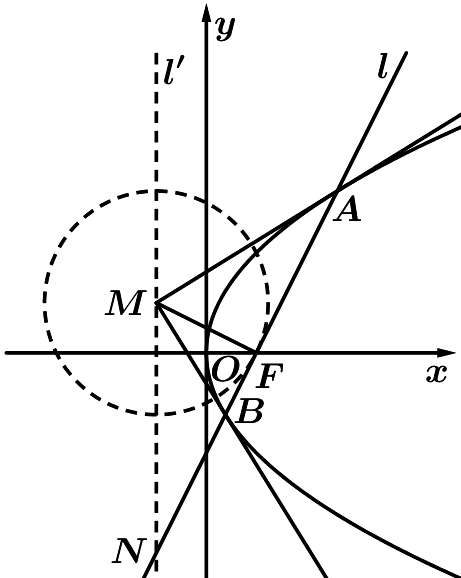
②设直线\(l\)与准线\({l}^{'}\)交于点\(N\)，若\(\left|MN\right|=\left|AB\right|\)，求直线\(l\)的方程.
题型：解答题 题类：月考试卷 难易度：较易
新年份：2021
已知\(\overrightarrow{a}\)，\(\overrightarrow{b}\)，\(\overrightarrow{c}\)是同一平面内的三个向量，其中\(\overrightarrow{a}=(1,\sqrt{3}).\)
\((1)\)若\(\left|\overrightarrow{c}\right|=4\)，且\(\overrightarrow{c}//\overrightarrow{a}\)，求\(\overrightarrow{c}\)的坐标；
\((2)\)若\(|\overrightarrow{b}|=1\)，且\((\overrightarrow{a}+\overrightarrow{b}){\rm⊥}(\overrightarrow{a}-\dfrac{5}{2}\overrightarrow{b})\)，求\(\overrightarrow{a}\)与\(\overrightarrow{b}\)的夹角\(θ.\)
题型：解答题 题类：月考试卷 难易度：较易
新年份：2021
某同学用“五点法”画函数\(f(x)=A\sin(\omega x+\varphi)+B(\)其中\(A>0\)，\(\omega>0\)，\(|\varphi|< \dfrac{\pi}{2})\)在某一个周期内的图象时，列表并填入部分数据，如表：
\(\omega x+\varphi\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(2\pi\) |
\(x\) | \(\dfrac{\pi}{3}\) | \(\dfrac{5\pi}{6}\) | |||
\(A\sin(\omega x+\varphi)+B\) | \(3\) | \(-1\) |
题型：解答题 题类：月考试卷 难易度：较易
新年份：2021
如图，\(MON\)是某景区的瀑布群，已知\(\tan∠MON=-\dfrac{4}{3}\)，点\(Q\)到直线\(OM\)，\(ON\)的距离均为\(2\)，现新修一条自\(A\)经过\(Q\)的有轨观光直路并延伸交道路\(ON\)于点\(B.\)