题型：解答题 题类：期末考试 难易度：中档
新年份：2020
\(《\)九章算术\(》\)是我国古代数学名著，它在几何学中的研究比西方早\(1000\)多年，在\(《\)九章算术\(》\)中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵\((qian\:du);\)阳马指底面为矩形，一侧棱垂直于底面的四棱锥，鳖膈\((bie\:nao)\)指四个面均为直角三角形的四面体\(.\)如图在堑堵\(ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}\)中，\(AB\bot AC\)．
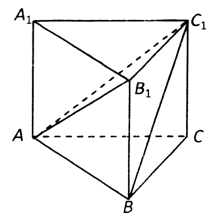
\((1)\)求证：四棱锥\(B-{{A}_{1}}AC{{C}_{1}}\)为阳马\(;\)
\((2)\)若\({{C}_{1}}C=BC=2\)，当鳖膈\({{C}_{1}}-ABC\)体积最大时，求锐二面角\(C-{{A}_{1}}B-{{C}_{1}}\)的余弦值．
题型：解答题 题类：期末考试 难易度：中档
新年份：2020
给定椭圆\(C: \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 ( a > b > 0 )\)，称圆心在原点\(O\)，半径为\(\sqrt{{{a}^{2}}+{{b}^{2}}}\)的圆是椭圆\(C\)的“卫星圆”\(.\)若椭圆\(C\)的离心率\(\dfrac{\sqrt{2}}{2}\)，点\(\left( 2,\sqrt{2} \right)\)在\(C\)上．
\((1)\)求椭圆\(C\)的方程和其“卫星圆”方程\(;\)
\((2)\)点\(P\)是椭圆\(C\)的“卫星圆”上的一个动点，过点\(P\)作直线\({{l}_{1}}\)，\({{l}_{2}}\)使得\({{l}_{1}} \bot {{l}_{2}}\)，与椭圆\(C\)都只有一个交点，且\({{l}_{1}}\)，\({{l}_{2}}\)分别交其“卫星圆”于点\(M\)，\(N\)，证明：弦长\(\left| MN \right|\)为定值．
题型：解答题 题类：期末考试 难易度：中档
新年份：2020
题型：解答题 题类：期末考试 难易度：中档
新年份：2020
如图，在三棱柱\(ABC-A _{1} B _{1} C _{1}\)中，侧面\(ABB _{1} A _{1}\)和侧面\(BCC _{1} B _{1}\)都是边长为\(2\)的菱形，且\(∠BAA _{1} =∠CBB _{1} = \dfrac {π}{3}\)．