题型：填空题 题类：月考试卷 难易度：较难
年份：2018
\((1)\)若球的表面积为\(36\pi\)，则该球的体积等于______ ．
\((2)\)设数列\(\{ a_{n}\}\)为公差不为\(0\)的等差数列，\(a_{1}{=}1\)，且\(a_{1}\)，\(a_{3}\)，\(a_{6}\)成等比数列，则数列\(\{ a_{n}\}\)的前\(8\)项和\(S_{8}\)等于______ ．
\((3)\) 若对\(x{ > }0\)，\(y{ > }0\)有\((x{+}2y)(\dfrac{2}{x}{+}\dfrac{1}{y}){\geqslant }m\)恒成立，\(m\)的取值范围是______ ．
\((4)\)给出下列命题：\(①\)若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；\(②\)若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；\(③\)若两条平行直线中的一条垂直于直线\(m\)，那么另一条直线也与直线\(m\)垂直；其中，所有真命题的序号为______．
题型：解答题 题类：月考试卷 难易度：较难
年份：2018
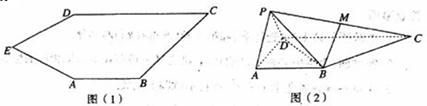
\((1)\)求证：平面\(PAD\bot \)平面\(ABCD\)；
\((2)\)若直线\(PC\)与\(AB\)所成角的正切值为\(\dfrac{1}{2}\)，求直线\(BM\)与平面\(PDB\)所成角的正弦值．
题型：填空题 题类：模拟题 难易度：较难
年份：2018
题型：填空题 题类：月考试卷 难易度：较难
年份：2018
\((1)\)棱长为\(2\)的正方体的外接球的表面积是__________
\((2)\)已知向量\(\overrightarrow{AB}\)与\(\overrightarrow{AC}\)的夹角为\(120^{\circ}\)，且\(\left| \overrightarrow{AB} \right|=3\)，\(\left| \overrightarrow{AC} \right|=2\)，若\(\overrightarrow{AP}=\lambda \overrightarrow{AB}+\overrightarrow{AC}\)，且\(\overrightarrow{AP}\bot \overrightarrow{BC}\)，则实数\(\lambda \)的值为__________．
\((3)α,β \)是两个平面，\(m\)，\(n\)是两条直线，有下列四个命题：
\((1)\)如果\(m⊥n,m⊥α,n/\!/β \)，那么\(α⊥β \)．
\((2)\)如果\(m⊥α,n/\!/α \)，那么\(m⊥n \)．
\((3)\)如果\(α/\!/β,m⊂α \)，那么\(m/\!/β \)．
\((4)\)如果\(m/\!/n,α/\!/β \)，那么\(m\)与\(α \)所成的角和\(n\)与\(β \)所成的角相等．
其中正确的命题有_______\(.(\)填写所有正确命题的编号\()\)
\((4)\) 设等比数列\({ }\!\!\{\!\!{ }{{a}_{n}}{ }\!\!\}\!\!{ }\)满足\(a_{1}+a_{3}=10\)，\(a_{2}+a_{4}=5\)，则\(a_{1}a_{2}\cdot \cdot \cdot a_{n}\)的最大值为___________．
题型：解答题 题类：其他 难易度：较难
年份：2018
如图，在四面体\(ABCD\)中，截面\(PQMN\)是正方形，则在下列命题中，错误的为\((\) \()\) 