题型:解答题 题类:期末考试 难易度:难
年份:2018
如图,在三棱柱\(ABC-{A}_{1}{B}_{1}{C}_{1} \)中,\(AB⊥ \)平面\(A{A}_{1}{C}_{1}C \),\(A{A}_{1}=AC .\)过\(A{A}_{1} \)的平面交\({B}_{1}{C}_{1} \)于点\(E\),交\(BC\)于点\(.F\)
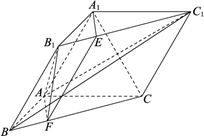
\((\)Ⅰ\()\)求证:\({A}_{1}C⊥ \)平面\(AB{C}_{1} \);
\((\)Ⅱ\()\)记四棱锥\({B}_{1}-A{A}_{1}EF \)的体积为\({V}_{1} \),三棱柱\(ABC-{A}_{1}{B}_{1}{C}_{1} \)的体积为\(V.\)若\(BF=FC\),证明\({{B}_{1}}E=E{{C}_{1}}\),并求\(\dfrac{{{V}_{1}}}{V}\)的值
题型:解答题 题类:期末考试 难易度:较易
年份:2018
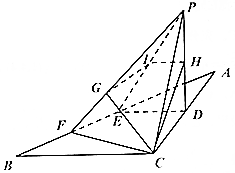 如图,\(\triangle ABC\)中,\(AC=2\),\(BC=4\),\(∠ACB=90^{\circ}\),\(D\)、\(E\)分别是\(AC\)、\(AB\)的中点,将\(\triangle ADE\)沿\(DE\)折起成\(\triangle PDE\),使面\(PDE⊥\)面\(BCDE\),\(H\)、\(F\)分别是边\(PD\)和\(BE\)的中点,平面\(BCH\)与\(PE\)、\(PF\)分别交于点\(I\)、\(G\).
如图,\(\triangle ABC\)中,\(AC=2\),\(BC=4\),\(∠ACB=90^{\circ}\),\(D\)、\(E\)分别是\(AC\)、\(AB\)的中点,将\(\triangle ADE\)沿\(DE\)折起成\(\triangle PDE\),使面\(PDE⊥\)面\(BCDE\),\(H\)、\(F\)分别是边\(PD\)和\(BE\)的中点,平面\(BCH\)与\(PE\)、\(PF\)分别交于点\(I\)、\(G\).题型:解答题 题类:期末考试 难易度:较难
年份:2018
