代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1542选择本页全部试题

题型：解答题题类：历年真题难易度：中档

年份：2018

已知\(\{a_{n}\}\)是等比数列，\(\{b_{n}\}\)是公差不为零的等差数列，且\(a_{1}=b_{1}=1\)，\(a_{2}=b_{2}\)，\(a_{3}=b_{5}\)
\((1)\)求数列\(\{a_{n}\}\)，\(\{b_{n}\}\)的通项公式；
\((2)\)设\(c_{n}= \dfrac {b_{n}}{a_{n}}\)，且\(\{c_{n}\}\)的前\(n\)项的和为\(T_{n}\)，求证：\(T_{n} < 3\)

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

等差数列\(\{a_{n}\}\)的前\(n\)项和为\(S_{n}\)，数列\(\{b_{n}\}\)是等比数列，满足\(a_{1}=3\)，\(b_{1}=1\)，\(b_{2}+S_{2}=10\)，\(a_{5}-2b_{2}=a_{3}\)．
\((\)Ⅰ\()\)求数列\(\{a_{n}\}\)和\(\{b_{n}\}\)的通项公式；
\((\)Ⅱ\()\)令\(Cn= \begin{cases} \dfrac {2}{S_{n}},n{为奇数} \\ b_{n,}n{为偶数}\end{cases}\)设数列\(\{c_{n}\}\)的前\(n\)项和\(T_{n}\)，求\(T_{2n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易

年份：2018

如图所示，在四棱锥\(P-ABCD\)中，底面\(AB-CD\)是正方形，侧棱\(PD⊥\)底面\(ABCD\)，\(PD=DC=2\)，\(E\)是\(PC\)的中点．

\((1)\)证明：\(PA/\!/\)平面\(EDB\)；

\((2)\)求三棱锥\(A-BDP\)的体积．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：易

年份：2018

如图，在四棱锥\(P-ABCD\)中，\(O\)为\(AC\)与\(BD\)的交点，\(AB⊥\)平面\(PAD\)，\(\triangle PAD\)是正三角形， \(DC/\!/AB\)，\(DA=DC=2AB\)．

\((1)\)若点\(E\)为棱\(PA\)上一点，且\(OE/\!/\)平面\(PBC\)，求\( \dfrac{AE}{PE}\)的值；

\((2)\)求证：平面\(PBC⊥\)平面\(PDC\)．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

设不等式\(|2x-1| < 1\)的解集为\(M\)，且\(a\)\(\in \)\(M\)，\(b\)\(\in \)\(M.\)
\((1)\)试比较\(ab+1\)与\(a+b\)的大小；

\((2)\)设\(max A\)表示数集\(A\)中的最大数，且\(h=max\)\(\left\{ \dfrac{2}{ \sqrt{a}}, \dfrac{a+b}{ \sqrt{ab}}, \dfrac{2}{ \sqrt{b}}\right\} \)，求\(h\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难

年份：2018

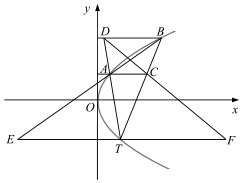如图，在平面直角坐标系\(xOy\)中，已知点\(T(1,t)(t < 0)\)到抛物线\(y^{2}=2px(p > 0)\)焦点的距离为\(2\)．
\((1)\)求\(p\)，\(t\)的值；
\((2)\)设\(A\)，\(B\)是抛物线上异于\(T\)的两个不同点，过\(A\)作\(y\)轴的垂线，与直线\(TB\)交于点\(C\)，过\(B\)作\(y\)轴的垂线，与直线\(TA\)交于点\(D\)，过\(T\)作\(y\)轴的垂线，与直线\(AB\)，\(CD\)分别交于点\(E\)，\(F\)．
求证：\(①\)直线\(CD\)的斜率为定值；
\(②T\)是线段\(EF\)的中点．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

已知向量\(a=(2λ\sin x,\sin x+\cos x)\)，向量\(b=(\sqrt{3}\cos x,λ(\sin x-\cos x))(λ > 0)\)，函数\(f(x)=a·b\)的最大值为\(2\)．
\((1)\)求函数\(f(x)\)的单调递减区间；
\((2)\)在\(\triangle ABC\)中，内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，\(\cos A=\dfrac{2b-a}{2c}\)，若\(f(A)-m > 0\)恒成立，求实数\(m\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：难

年份：2018

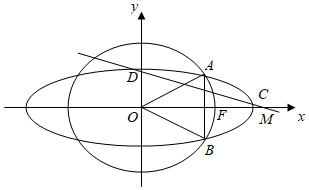已知椭圆\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)的右焦点为\(F(2,0)\)，以原点\(O\)为圆心，\(OF\)为半径的圆与椭圆在\(y\)轴右侧交于\(A\)，\(B\)两点，且\(\triangle AOB\)为正三角形．
\((I)\)求椭圆方程；
\((\)Ⅱ\()\)过圆外一点\(M(m,0)(m > a)\)，作倾斜角为\( \dfrac {5}{6}π\)的直线\(l\)交椭圆于\(C\)，\(D\)两点，若点\(F\)在以线段\(CD\)为直径的圆\(E\)的内部，求\(m\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较难

年份：2018

已知各项均为正数的等差数列\(\{a_{n}\}\)满足\(a_{4}=2a_{2}\)，且\(a_{1}\)，\(4\)，\(a_{4}\)成等比数列，设\(\{a_{n}\}\)的前\(n\)项和为\(S_{n}\)．
\((1)\)求数列\(\{a_{n}\}\)的通项公式\(;\)
\((2)\)设数列\(\left\{ \dfrac{S_{n}}{n\mathrm{{·}}2^{n}} \right\}\)的前\(n\)项和为\(T_{n}\)，求证：\(T_{n} < 3\)

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易

年份：2018

如图所示，在四棱锥\(P -ABCD\)中， \(∠ABC=∠ACD=90^{\circ}\)， \(∠BAC =∠CAD=60^{\circ}\)，\(PA⊥\)平面\(ABCD\)，\(PA=2\)，\(AB=1.\)设\(M\)，\(N\)分别为\(PD\)，\(AD\)的中点．

\((1)\)求证：平面\(CMN/\!/\)平面\(PAB;\)

\((2)\)求三棱锥\(P -ABM\)的体积．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心