选择章节

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：82 选择本页全部试题

题型：解答题题类：期末考试难易度：中档

年份：2018

如图，斜三棱柱\(ABC-A_{1}B_{1}C_{1}\)的底面是直角三角形，\(AC⊥CB\)，\(∠ABC=45^{\circ}\)，侧面\(A_{1}ABB_{1}\)是边长为\(a\)的菱形，且垂直于底面\(ABC\)，\(∠A_{1}AB=60^{\circ}\)，\(E\)、\(F\)分别是\(AB_{1}\)、\(BC\)的中点．

\((1)\)求证\(EF/\!/\)平面\(A_{1}ACC_{1}\)；
\((2)\)求\(EF\)与侧面\(A_{1}ABB_{1}\)所成的角．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：较易

年份：2018

在等腰梯形\({ABCD}\)中，\(AB{/\!/}CD\)，直线\(FC⊥面ABCD \)，\(ED{/\!/}FC\)，点\(G\)为\({AB}\)的中点，且\(FC{=}AB{=}2ED{=}2CD{=}2\)，\({∠}ABC{=}60^{0}\)．

\((1)\)求异面直线\(ED\)与\(BF\)所成交的正切值

\((2)\)求证：平面\(ACF\bot \)平面\({BCF}\)；

\((3)\)求直线\({FB}\)与平面\({ADE}\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：中档

年份：2018

在如图所示的几何体中，PB∥EC，PB=2CE=2，PB⊥平面ABCD，在平行四边形ABCD中，AB=1，AD=2，∠BAD=60°．
（1）求证：AC∥平面PDE；
（2）求CD与平面PDE所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：中档

年份：2018

四棱锥\(P-ABCD\)中，底面\(ABCD\)是矩形，\(PA\bot \)底面\(ABCD\)，\(PA=AB=1\)，\(AD=\sqrt{3}\)，点\(F\)是\(PB\)的中点，点\(E\)在边\(BC\)上移动．

\((1)\)证明：无论点\(E\)在边\(BC\)的何处，都有\(PE\bot AF;\)

\((2)\)当\(BE\)等于何值时，\(PA\)与平面\(PDE\)所成角的大小为\({{45}^{\circ }}\)．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：较易

年份：2018

如图，已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，且AB=BP=2，AD=AE=1，AE⊥AB，且AE∥BP．
（1）求平面PCD与平面ABPE所成的二面角的余弦值；
（2）线段PD上是否存在一点N，使得直线BN与平面PCD所成角的正弦值等于？若存在，试确定点N的位置；若不存在，请说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：较难

年份：2018

如图，三棱柱\(ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}\)中，底面\(ABC\)为等腰直角三角形，\(AB=AC=1\)，\(B{{B}_{1}}=2\)，\(\angle AB{{B}_{1}}={{60}^{\circ }}\)．

\((\)Ⅰ\()\)证明：\(AB\bot {{B}_{1}}C\)；

\((\)Ⅱ\()\)若\({{B}_{1}}C=2\)，求\(A{{C}_{1}}\)与平面\(BC{{B}_{1}}\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：较难

年份：2018

如图所示，在三棱锥\(A-BCD\)中，\(AB⊥\)平面\(BCD\)，\(AC=AD=2\)，\(BC=BD=1\)，点\(E\)是线段\(AD\)的中点．

\((1)\)如果\(CD=\sqrt{2}\)，求证：平面\(BCE⊥\)平面\(ABD\)．

\((2)\)如果\(\angle CBD=\dfrac{2\pi }{3}\)，求直线\(CE\)和平面\(BCD\)所成的角的余弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：较难

年份：2018

如图所示，在四棱锥\(P-ABCD\)中，底面四边形\(ABCD\)是菱形，\(AC∩BD=O \)，\(∆PAC \)是边长为\(2\)的等边三角形，\(PB=PD= \sqrt{6} \)，\(AP=4AF\)．

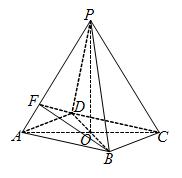
\((1)\)求证：\(PO⊥ \)底面\(ABCD\)；

\((2)\)求直线\(CP\)与平面\(BDF\)所成角的大小；

\((3)\)在线段\(PB\)上是否存在一点\(M\)，使得\(CM/\!/ \)平面\(BDF\)？如果存在，求\( \dfrac{BM}{BP} \)的值，如果不存在，请说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：难

年份：2018

如图，四棱锥\(P-ABCD\)的底面是正方形，\(PA⊥\)底面\(ABCD\)，\(PA=AB\)，点\(M\)，\(N\)分别在棱\(PD\)，\(PC\)上，且\(PC⊥\)平面\(AMN\)．

\((1)\)求证：\(AM⊥PD\)；

\((2)\)求直线\(CD\)与平面\(AMN\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期末考试难易度：易

年份：2018

如图，四棱锥\(S-ABCD\)中，\(AB/\!/CD\)，\(BC⊥CD\)，侧面\(SAB\)为等边三角形，\(AB=BC=2\)，\(CD=SD=1\)．

证明：\(SD⊥\)平面\(SAB\)；

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心