题型：解答题 题类：历年真题 难易度：较易
年份：2018
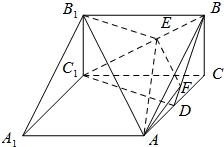如图，三棱柱\(ABC-A_{1}B_{1}C_{1}\)中，\(BC\)垂直于正方形\(A_{1}ACC_{1}\)所在平面，\(AC=2\)，\(BC=1\)，\(D\)为\(AC\)中点，\(E\)为线段\(BC_{1}\)上的一点\((\)端点除外\()\)，平面\(AB_{1}E\)与\(BD\)交于点\(F\) 题型：解答题 题类：历年真题 难易度：较易
年份：2018
题型：解答题 题类：历年真题 难易度：难
年份：2018
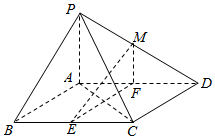如图，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是平行四边形，\(∠BCD=135^{\circ}\)，侧面\(PAB⊥\)底面\(ABCD\)，\(∠BAP=90^{\circ}\)，\(AB=AC=PA=2\)，\(E\)，\(F\)分别为\(BC\)，\(AD\)的中点，点\(M\)在线段\(PD\)上．
如图，在四棱锥\(P-ABCD\)中，侧面\(PAD⊥\)底面\(ABCD\)，底面\(ABCD\)是平行四边形，\(∠ABC=45^{\circ}\)，\(AD=AP=2\)，\(AB=DP=2 \sqrt {2}\)，\(E\)为\(CD\)的中点，点\(F\)在线段\(PB\)上．
如图，\(ABCD\)是边长为\(a\)的菱形，\(∠BAD=60^{\circ}\)，\(EB⊥\)平面\(ABCD\)，\(FD⊥\)平面\(ABCD\)，\(EB=2FD= \sqrt {3}a\) 
如图，在三棱锥\(P-ABC\)中，\(PA=AC=PC=AB=a\)，\(PA⊥AB\)，\(AC⊥AB\)，\(M\)为\(AC\)的中点．
在四棱锥\(P-ABCD\)中，\(PA⊥\)平面\(ABCD\)，\(AB⊥AD\)，\(BC/\!/AD\)，\(BC=1\)，\(CD= \sqrt {2},∠CDA=45 ^{\circ} \)． 
如图，菱\(ABCD\)与四边形\(BDEF\)相交于\(BD\)，\(∠ABC=120^{\circ}\)，\(BF⊥\)平面\(ABCD\)，\(DE/\!/BF\)，\(BF=2DE\)，\(AF⊥FC\)，\(M\)为\(CF\)的中点，\(AC∩BD=G\)．
如图，四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)的所有棱长都是\(2\)，\(O\)是\(AC\)与\(BD\)的交点，\(A_{1}O⊥AB\)，\(A_{1}O⊥BC\)．
如图，三棱柱\(ABC-A_{1}B_{1}C_{1}\)所有的棱长均为\(1\)，\(A_{1}C⊥B_{1}\)C. 