题型：解答题 题类：期末考试 难易度：较易
新年份：2021
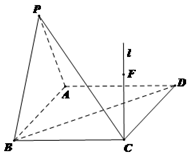已知矩形\(ABCD\)满足\(AB=2\)，\(BC=\sqrt{2}\)，\(\triangle PAB\)是正三角形，平面\(PAB⊥\)平面\(ABCD.\)题型：解答题 题类：期末考试 难易度：较易
新年份：2021
如图，在四棱锥\(P-ABCD\)中，平面\(PAB⊥\)平面\(ABCD\)，\(PA⊥AB\)，\(PA=AD=4\)，\(BC{\rm{/}}{\rm{/}}AD\)，\(AB⊥AD\)，\(AB=BC=2\)，\(\overrightarrow {PE}=λ\overrightarrow {PC}\left({0\leqslant λ< 1}\right).\)
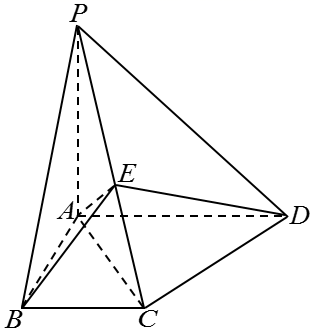
\((1)\)若\(λ=\dfrac{1}{2}\)，求直线\(DE\)与平面\(ABE\)所成角的正弦值；
\((2)\)设二面角\(B-AE-C\)的大小为\(θ\)，若\(\left|{\cos θ}\right|=\dfrac{2\sqrt[]{34}}{17}\)，求\(λ\)的值．
如图，三棱柱\(ABC-A_{1}B_{1}C_{1}\)的底面是边长为\(2\)的正三角形，侧面\(ACC_{1}A_{1}⊥\)底面\(ABC\)，且侧面\(ACC_{1}A_{1}\)为菱形，\(∠A_{1}AC=60°\)，\(E\)是\(BB_{1}\)的中点，\(F\)是\(AC_{1}\)与\(A_{1}C\)的交点.
如图，在多面体\(ABCDE\)中，\(DE/\!/AB\)，\(AC⊥BC\)，\(BC=2AC=2\)，\(AB=2DE\)，且\(D\)点在平面\(ABC\)内的正投影为\(AC\)的中点\(H\)且\(DH=1.\)
如图，边长为\(2\)的正方形\(ACDE\)所在平面与平面\(ABC\)垂直，\(AD\)与\(CE\)的交点为\(M\)，\(AC⊥BC\)，且\(AC=BC\)，
如图，在直三棱柱\(ABC-A_{1}B_{1}C_{1}\)中，\(∠BAC=90°\)，\(AB=AC=AA_{1}.\)
如图，已知四棱锥\(P-ABCD\)的底面是正方形，点\(E\)是棱\(PA\)的中点，\(PA⊥\)平面\(ABCD.\)
