题型：解答题 题类：其他 难易度：较易
新年份：2021
在①\(\angle PAB={{60}^{{}^\circ}}\)；②\(PA\bot PB\)；③\(\angle PAB={{120}^{{}^\circ}}\)这三个条件中任选一个，补充在下面问题中，若问题中的\(\lambda\)存在，求出\(\lambda\)的值；若\(\lambda\)不存在，请说明理由.
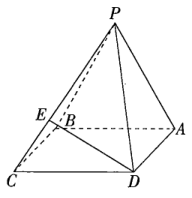
已知等腰三角形\(PAB\)和正方形\(ABCD\)，________，\(AB=1\)，平面\(PAB\bot\)平面\(ABCD\)，是否存在点\(E\)，满足\(\overrightarrow{PE}=\lambda\overrightarrow{PC}\)，使直线\(DE\)与平面\(PBC\)所成角为\(60°\)？
如图，四边形\(ABCD\)是直角梯形，\(∠ABC=∠DAB=90°\)，\(SA⊥\)平面\(ABCD\)，\(SA=AB=BC=1\)，\(AD= \dfrac {1}{2}\)，求直线\(SC\)与平面\(SBD\)所成角的正弦值． 
如图，正三棱柱\(ABC-A _{1} B _{1} C _{1}\)的底面边长为\(a\)，侧棱长为\( \sqrt {2}a\)．
如图所示，\(AF\)、\(DE\)分别是\(⊙O\)、\(⊙O _{1}\)的直径，\(AD\)与两圆所在的平面均垂直，\(AD=8\)，\(BC\)是\(⊙O\)的直径，\(AB=AC=6\)，\(OE/\!/AD\) 
已知几何体\(EFG-ABCD\)如图所示，其中四边形\(ABCD\)，\(CDGF\)，\(ADGE\)均为正方形，且边长为\(1\)，点\(M\)在边\(DG\)上．
