题型：解答题 题类：期中考试 难易度：中档
新年份：2020
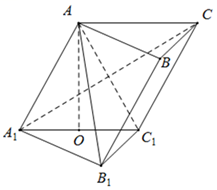如图，在斜三棱柱\(ABC-A _{1} B _{1} C _{1}\)中，点\(O\)、\(E\)分别是\(A _{1} C _{1}\)、\(A _{1} B _{1}\)的中点，\(A _{1} C\)与\(AC _{1}\)交于点\(F\)，\(AO⊥\)平面\(A _{1} B _{1} C _{1} .\)已知\(∠BCA=90°\)，\(AA _{1} =AC=BC=2\)．题型：解答题 题类：期中考试 难易度：中档
新年份：2020
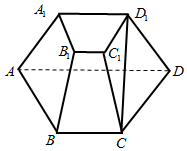如图，四棱台\(ABCD-A _{1} B _{1} C _{1} D _{1}\)中，底面\(ABCD\)与侧面\(AA _{1} B _{1} B\)为相似的等腰梯形，\(AD/\!/BC\)，\(AB=2\)，\(AD=4\)，\(∠BAD=60°\)．
如图，在四棱锥\(P-ABCD\)中，\(PA⊥\)平面\(ABCD\)，\(AD/\!/BC\)，\(AD⊥CD\)，且\(AD=CD= \sqrt {2}\)，\(BC=2 \sqrt {2}\)，\(PA=2\)．
如图，在四棱锥\(P-ABCD\)，底面\(ABCD\)为菱形，\(∠ABC=60°\)，\(PB=PC\)，\(E\)为线段\(BC\)的中点．
如图所示，在直三棱柱\(ABCA _{1} B _{1} C _{1}\)中，\(E\)，\(F\)分别为\(A _{1} C _{1}\)和\(BC\)的中点．
如图所示的多面体中，底面\(ABCD\)为矩形，\(BE⊥\)平面\(ABCD\)，\(CC _{1} ⊥\)平面\(ABCD\)，\(DF⊥\)平面\(ABCD\)，\(AF/\!/EC _{1}\)，且\(AB=4\)，\(BC=2\)，\(CC _{1} =3\)，\(BE=1\)．
如图，在正方体\(ABCD-A _{1} B _{1} C _{1} D _{1}\)中，\(E\)为棱\(DD _{1}\)的中点．求证：
如图，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是正方形，侧棱\(PD⊥\)底面\(ABCD\)，\(E\)是\(PC\)的中点．
如图，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是矩形，\(M\)是\(PA\)的中点，\(PD⊥\)平面\(ABCD\)，且\(PD=CD=4\)，\(AD=2\)．
如图，四棱锥\(P-ABCD\)中，\(PD⊥\)底面\(ABCD\)，\(AB/\!/CD\)，\(∠BAD= \dfrac {π}{3}\)，\(AB=1\)，\(CD=3\)，\(M\)为\(PC\)上一点，且\(MC=2PM\)，\(AD=2\)，\(PD=3\)．