选择章节

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：105 选择本页全部试题

题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，在三棱锥\(S-ABC\)中，\(SC⊥\)平面\(ABC\)，\(SC=3\)，\(AC⊥BC\)，\(CE=2EB=2\)，\(AC=\dfrac{3}{2}\)，\(CD=ED.\)
\((Ⅰ)\)求证：\(DE⊥\)平面\(SCD\)；
\((Ⅱ)\)求\(SB\)与平面\(SCD\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

在四棱锥\(S-ABCD\)中，底面\(ABCD\)为长方形，\(SB⊥\)底面\(ABCD\)，其中\(BS=2\)，\(BA=2\)，\(BC=t\)，\(t\)的可能取值为：①\(t=\dfrac{1}{3}\)；②\(t=\dfrac{\sqrt{2}}{2}\)；③\(t=\dfrac{\sqrt{3}}{2}\)；④\(t=\dfrac{5}{2}\)；⑤\(t=3.\)

\((1)\)求直线\(AS\)与平面\(ABCD\)所成角的正弦值；
\((2)\)若线段\(CD\)上能找到点\(E\)，满足\(AE⊥SE\)，则\(t\)可能的取值有几种情况？请说理由；
\((3)\)在\((2)\)的条件下，当\(t\)为所有可能情况的最大值时，线段\(CD\)上满足\(AE⊥SE\)的点有两个，分别记为\(E_{1}\)，\(E_{2}\)，求二面角\(E_{1}-SB-E_{2}\)的大小.

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，在四棱锥\(P-ABCD\)中，底面\(ABCD\)是矩形，\(PA\bot AB\)，\(AB=2BC=2\)，\(PC=3\)，\(PA=2\)，\(E\)为\(PD\)的中点．
\((1)\)证明：\(BC\bot\)平面\(PAB\)；
\((2)\)求直线\(EB\)与平面\(PBC\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图所示多面体中，\(AD⊥\)平面\(PDC\)，四边形\(ABCD\)为平行四边形，\(E\)为\(AD\)的中点，\(F\)为线段\(BP\)上一点，\(∠CDP=120°\)，\(AD=3\)，\(AP=5\)，\(CD=2.\)
\((1)\)若\(F\)为\(BP\)的中点，证明：\(EF/\!/\)平面\(PDC\)；
\((2)\)若\(BF=\dfrac{1}{3}BP\)，求直线\(AF\)与平面\(PBC\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，已知\(PA⊥\)平面\(ABCD\)，\(ABCD\)为矩形，\(PA=AD=AB=2\)，\(M\)，\(N\)分别为\(AB\)，\(PC\)的中点，求证：
\((1)MN/\!/\)平面\(PAD\)；
\((2)\)求\(PD\)与平面\(PMC\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

已知多面体\(ABCDE\)中，\(DE⊥\)平面\(ACD\)，\(AB/\!/DE\)，\(AC=AD=CD=DE=2\)，\(AB=1\)，\(O\)为\(CD\)的中点．
\((Ⅰ)\)求证：\(AO/\!/\)平面\(BCE\)；
\((Ⅱ)\)求异面直线\(AC\)和\(BE\)所成角的余弦值；
\((Ⅲ)\)求直线\(BD\)与平面\(BCE\)所成角的正弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

在如图所示的多面体中，\(EA\bot\)平面\(ABC\)，\(DB\bot\)平面\(ABC\)，\(AC\bot BC\)，且\(AC=BC=BD=2AE=2\)，\(M\)是\(AB\)的中点．
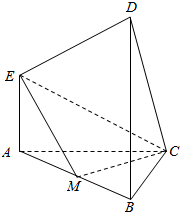
\((1)\)求证：\(CM\bot EM\)；
\((2)\)求平面\(EMC\)与平面\(BCD\)所成的锐二面角的余弦值；
\((3)\)在棱\(DC\)上是否存在一点\(N\)，使得直线\(MN\)与平面\(EMC\)所成的角为\(60{}^\circ\)，若存在，指出点\(N\)的位置；若不存在，请说明理由．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

在四棱锥\(P-ABCD\)中，\(AD//BC\)，\(AD=AB=1\)，\(BC=2\)，\(BD=\sqrt{2}\)，\(E\)为\(PB\)的中点.
\((1)\)证明：\(AE//\)平面\(PCD\)；
\((2)\)若\(PA\bot\)平面\(ABCD\)，且\(PA=\sqrt{3}\)，求\(CP\)与平面\(PBD\)所成角的正弦值.

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，四棱锥\(P-ABCD\)的底面\(ABCD\)是边长为\(2\)的菱形，\(PA⊥\)底面\(ABCD\)，\(∠BAD=120°\)，\(E\)，\(F\)分别是\(CD\)，\(PC\)的中点，\(AP=4.\)
\((1)\)求四棱锥\(F-ABCE\)的体积；
\((2)\)求\(BF\)与底面\(ABCD\)所成角的正切值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：较易
新
年份：2021

如图，在三棱锥\(P-ABC\)中，\(PA⊥\)平面\(ABC\)，\(∠BAC=90°\)，\(D\)，\(E\)，\(F\)分别是棱\(AB\)，\(BC\)，\(CP\)的中点，\(AB=AC=PA=2.\)

\((1)\)求直线\(PA\)与平面\(DEF\)所成角的正弦值；
\((2)\)求点\(P\)到平面\(DEF\)的距离.

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心