题型:解答题 题类:期末考试 难易度:难
年份:2018
如图,在四棱锥\(P-ABCD\)中,\(AD/\!/BC,\angle ADC=\angle PAB={{90}^{\circ }},BC=CD=\dfrac{1}{2}AD,E\)为棱\(AD\)的中点,异面直线\(PA\)与\(CD\)所成的角为\(\dfrac{\pi }{2}\).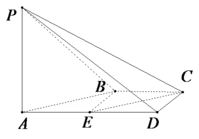
\((1)\)在平面\(PAB\)内找一点\(M\),使得直线\(CM/\!/\)平面\(PBE\),并说明理由.
\((2)\)若二面角\(P-CD-A\)的大小为\(\dfrac{\pi }{4}\),求直线\(PA\)与平面\(PCE\)所成角的正弦值.
题型:解答题 题类:期末考试 难易度:难
年份:2018
题型:解答题 题类:期末考试 难易度:难
年份:2018

题型:解答题 题类:期末考试 难易度:难
年份:2018
如图,在直角梯形\(ABCD\)中,\(AD/\!/BC\),\(\angle BAD={{90}^{\circ }}\),\(AB=BC=1\),\(AD=2\),\(E\)是\(AD\)的中点,\(O\)是\(AC\)与\(BE\)的交点,将\(ABE\)沿\(BE\)折起到\({{A}_{1}}BE\)的位置,如图\(2\).
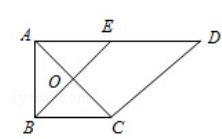
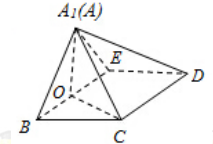
图\(1\) 图\(2\)
\((1)\)证明:\(CD\bot \)平面\({{A}_{1}}OC\);
\((2)\)若平面\({{A}_{1}}BE\bot \)平面\(BCDE\),求\(BC\)与平面\(A_{1}CD\)所成的角.
题型:解答题 题类:期末考试 难易度:难
年份:2018
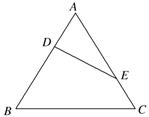
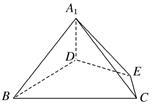
如图甲,在\(Rt\triangle ABC\)中,\(∠C=90^{\circ}\),\(BC=3\),\(AC=6\),\(D\),\(E\)分别为\(AC\),\(AB\)上的点,且\(DE/\!/BC\),\(DE=2\),将\(\triangle ADE\)沿\(DE\)折起到\(\triangle A_{1}DE\)的位置,使\(A1C⊥CD\),如乙图.
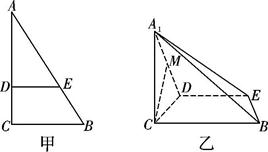
\((\)Ⅰ\()\)求证:\(A_{1}C⊥\)平面\(BCDE\);
\((\)Ⅱ\()\)若\(M\)是\(A_{1}D\)的中点,求\(CM\)与平面\(A_{1}BE\)所成角的大小.