选择章节

已知定义在\((-1,1)\)上的奇函数\(f(x)=\dfrac{ax+b}{{x}^{2}+1}\)是增函数，且\(f(\dfrac{1}{2})=\dfrac{2}{5}.\)

\((1)\)求函数\(f(x)\)的解析式；

\((2)\)解不等式\(f(t-1)+f(2t)< 0.\)

若函数\(f(x)\)的定义域为\(R\)，满足对任意\(x_{1}\)，\(x_{2}\in R\)，有\(f(x_{1}+x_{2})\leqslant f(x_{1})+f(x_{2})\)，则称\(f(x)\)为\(V\)型函数；若函数\(g(x)\)的定义域为\(R\)，满足对任意\(x\in R\)，\(g(x)>0\)恒成立，且对任意\(x_{1}\)，\(x_{2}\in R\)，有\(\lg\:g(x_{1}+x_{2})\leqslant\lg\:g(x_{1})+\lg\:g(x_{2})\)，则称\(g(x)\)为对数\(V\)型函数．

\((1)\)当函数\(f(x)=x^{2}\)时，判断\(f(x)\)是否为\(V\)型函数，并说明理由．

\((2)\)当函数\(g(x)=x^{2}+2\)时，证明：\(g(x)\)是对数\(V\)型函数．

\((3)\)若函数\(f(x)\)是\(V\)型函数，且满足对任意\(x\in R\)，有\(f(x)\geqslant 2\)，问\(f(x)\)是否为对数\(V\)型函数？若是，加以证明；若不是，请说明理由．

某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出\(1\)盒该产品获利润\(50\)元；未售出的产品，每盒亏损\(30\)元\(.\)根据历史资料，得到开学季市场需求量的频率分布直方图，如下图所示。该同学为这个开学季购进了\(160\)盒该产品，以\(x(\)单位：盒，\(100\leqslant x\leqslant 200)\)表示这个开学季内的市场需求量，\(y(\)单位：元\()\)表示这个开学季内经销该产品的利润。

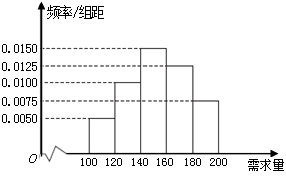
\((\)Ⅰ\()\)根据直方图估计这个开学季内市场需求量\(x\)的中位数；

\((\)Ⅱ\()\)将\(y\)表示为\(x\)的函数，并根据直方图估计利润不少于\(6400\)元的概率。

对于定义域为\(D\)的函数\(y=f(x)\)，若同时满足下列条件：\(①\)\(f(x)\)在\(D\)内单调递增或单调递减；\(②\)存在区间\([a,b]\subseteq D\)，使\(f(x)\)在\([a,b]\)上的值域为\([a,b]\)；那么把\(y=f(x)\)\((\)\(x\in D\)\()\)叫闭函数，则条件\(②\)中的区间\([a,b]\)为\(f(x)\)的一个“好区间”．

\((1)\)求闭函数\(y=-{{x}^{3}}\)的“好区间”；

\((2)\)若\([1,16]\)为闭函数\(f(x)=m\sqrt{x}+n{{\log }_{2}}x\)的“好区间”，求\(m\)、\(n\)的值．

已知\(x=1\)是函数\(f(x)=m{{x}^{3}}-3(m+1){{x}^{2}}+nx+1\) \((m < 0)\)的一个极值点，

\((1)\)求\(m\)与\(n\)的关系式；    

\((2)\)求\(f(x)\)的单调区间；      

\((3)\) 当\(x\in [-1,1]\)时， 函数\(y=f(x)\)的图象上任意一点的切线斜率恒大于\(3m\)， 求\(m\)的取值范围。