题型：填空题 题类：月考试卷 难易度：难
年份：2018
\((1)\)已知不等式组\(\begin{cases}\begin{matrix}y\leqslant x \\ y\geqslant -x\end{matrix} \\ x\leqslant a\end{cases} \)表示的平面区域\(S\)的面积为\(4\)，则\(z=2x+y\)的最大值为_____．
\((2)\)将数列\(\left\{ {{a}_{n}} \right\}\)按如图所示的规律排成一个三角形表，并同时满足以下两个条件：
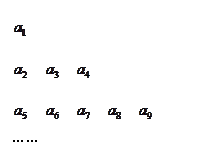
\(①\)各行的第一个数\({{a}_{1}},{{a}_{2}},{{a}_{5}}\)构成公差为\(d\)的等差数列；
\(②\)从第二行起，每行各数按从左到右的顺序构成公比为\(q\)的等比数列．
若\({{a}_{1}}=1,{{a}_{3}}=4,a_{5}^{{}}=3\)，则第\(n\)行的和\({{T}_{n}}=\)________
\((3)\)湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个直径为\(12 cm\)，深\(2cm\)的空穴，则该球的表面积是_____\(cm²\)．
\((4)\)已知\(\Delta ABC\)的外接圆半径为\(R\)，且\(2R({{\sin }^{2}}A-{{\sin }^{2}}C)=(\sqrt{2}a-b)\sin B.\) 则\(\angle C=\)____
题型：填空题 题类：月考试卷 难易度：难
年份：2018
\((1)\)若关于\(x\)的不等式\(-\dfrac{1}{2}{{x}^{2}}+2x > -mx\)的解集\(\{x|0 < x < 2\}\)，则\(m=\)______________。
\((2)\)设正项等比数列\(\{{{a}_{n}}\}\)的前\(n\)项和为\({{S}_{n}}\)，若\({{S}_{3}}=3,{{S}_{9}}-{{S}_{6}}=12\)，则\({{S}_{6}}=\)___________。
\((3)\)若正数\(x\)，\(y\)满足\(x+3y=xy\)，则\(3x+4y\)的最小值是________
\((4)\)给出以下四个命题：\(①\) 若\(\cos \alpha \cos \beta =1\)，则\(\sin (\alpha +\beta )=0\)；\(②\) 已知直线\(x=m\)与函数\(f(x)=\sin x,g(x)=\sin (\dfrac{\pi }{2}-x)\)的图像分别交于点\(M,N\)，则\(|MN|\)的最大值为\(\sqrt{2}\)；\(③\) 若数列\({{a}_{n}}={{n}^{2}}+\lambda n(n\in {{N}_{+}})\)为单调递增数列，则\(\lambda \)取值范围是\(\lambda > -2\)；\(④\) 已知数列\(\{{{a}_{n}}\}\)的通项\({{a}_{n}}=\dfrac{3}{2n-11}\)，其前\(n\)项和为\({{S}_{n}}\)，则使\({{S}_{n}} > 0\)的\(n\)的最小值为\(12.\)其中正确命题的序号为_____________．
的前n项和为Sn，已知S2017=5710，S2018=4030，若数列{an}为等差数列，则S2019=______． 
，数列的{bn}的前n项和为Tn，则满足Tn＞1024的最小n的值为______． 
，n∈N*．记数列{an}的前n项和为Sn，则S2019=______． 