题型：选择题 题类：期中考试 难易度：较易
新 测年份：2021
攒尖是古代中国建筑中屋顶的一种结构形式，宋代称为撮尖，清代称攒尖．依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，也有单檐和重檐之分，多见于亭阁式建筑．如图所示，某园林建筑的屋顶为六角攒尖，它的主要部分的轮廓可近似看作一个正六棱锥，若此正六棱锥的侧棱长为\(2\)，且与底面所成的角为\(\dfrac{π}{6}\)，则此正六棱锥的体积为\((\quad)\) 题型：解答题 题类：期中考试 难易度：较易
新年份：2021
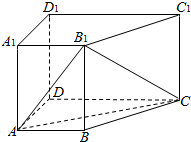如图，在四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，侧棱\(AA_{1}⊥\)底面\(ABCD\)，\(AB/\!/DC\)，\(AA_{1}=1\)，\(AB=3k\)，\(AD=4k\)，\(BC=5k\)，\(DC=6k\)，\((k>0)\)题型：解答题 题类：期中考试 难易度：较易
新年份：2021
如图，在棱长为\(2\)的正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，\(P\)，\(Q\)分别为\(CC_{1}\)，\(B_{1}C_{1}\)的中点，则过\(D\)，\(P\)，\(Q\)三点的平面截正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)所得截面的面积为 ______. 
如图，在直四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，底面\(ABCD\)为正方形，\(AA_{1}=2AB=4\)，\(M\)，\(N\)，\(P\)分别是\(AD\)，\(DD_{1}\)，\(CC_{1}\)的中点．