在数列{a
n}中，若a
n2-a
n-12=D（n≥2，n∈N
*，D为常数），则称{a
n}为“平方等差数列”．
（Ⅰ）若数列{b
n}是“平方等差数列”，b
1=1，b
2=2，写出b
3，b
4的值；
（Ⅱ）如果一个公比为q的等比数列为“平方等差数列”，求证：q=±1；
（Ⅲ）若一个“平方等差数列”{c
n}满足c
1=2，c
2=2
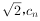
＞0，设数列
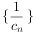
的前n项和为T
n．是否存在正整数p，k，使不等式T
n＞
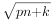
-1对一切n∈N
*都成立？若存在，求出p，k的值；若不存在，说明理由．
，b1+b2+b3=21，b1b2b3=315．
，数列{bn}的前n项和为Tn，求Tn． 
，
，求证：数列{cn}是等差数列；
的前n项和为Sn，求证：
． 
，且a1bm+a2bm-1+a3bm-2+…+amb1=12-2m，求m的值 