选择章节

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：72 选择本页全部试题

题型：解答题题类：历年真题难易度：中档

年份：2018

已知\(\{a_{n}\}\)是等比数列，\(\{b_{n}\}\)是公差不为零的等差数列，且\(a_{1}=b_{1}=1\)，\(a_{2}=b_{2}\)，\(a_{3}=b_{5}\)
\((1)\)求数列\(\{a_{n}\}\)，\(\{b_{n}\}\)的通项公式；
\((2)\)设\(c_{n}= \dfrac {b_{n}}{a_{n}}\)，且\(\{c_{n}\}\)的前\(n\)项的和为\(T_{n}\)，求证：\(T_{n} < 3\)

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

已知等比数列\(\{a_{n}\}\)的公比\(q\neq 1\)，前\(n\)项和为\(S_{n}\)，\(a_{1}+a_{3}= \dfrac {S_{4}}{S_{2}}\)，\(a_{1}-1\)，\(a_{2}-1\)，\(a_{3}-1\)分别是一个等差数列的第\(1\)项，第\(2\)项，第\(5\)项．
\((\)Ⅰ\()\)求数列\(\{a_{n}\}\)的通项公式；
\((\)Ⅱ\()\)设\(b_{n}=a_{n}\lg a_{n}\)，求数列\(\{b_{n}\}\)的前\(n\)项和\(T_{n}\)．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

等差数列\(\{a_{n}\}\)的前\(n\)项和为\(S_{n}\)，数列\(\{b_{n}\}\)是等比数列，满足\(a_{1}=3\)，\(b_{1}=1\)，\(b_{2}+S_{2}=10\)，\(a_{5}-2b_{2}=a_{3}\)．
\((\)Ⅰ\()\)求数列\(\{a_{n}\}\)和\(\{b_{n}\}\)的通项公式；
\((\)Ⅱ\()\)令\(Cn= \begin{cases} \dfrac {2}{S_{n}},n{为奇数} \\ b_{n,}n{为偶数}\end{cases}\)设数列\(\{c_{n}\}\)的前\(n\)项和\(T_{n}\)，求\(T_{2n}\)．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

已知S_n是数列{a_n}前n项和，a₁=1，2S_n=（n+1）a_n（n∈N*）．
（1）求数列{a_n}的通项公式；
（2）若a_na_n+1b_n=1，T_n是数列{b_n}前n项和，求T_n．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

已知数列\(\left\{ {{a}_{n}} \right\}\)的前\(n\)项和为\(S_{n}\)，且\(1\)，\(a_{n}\)，\(S_{n}\)成等差数列．

\((1)\)求数列\(\left\{ {{a}_{n}} \right\}\)的通项公式；

\((2)\)若数列\(\left\{ {{b}_{n}} \right\}\)满足\({{a}_{n}}\cdot {{b}_{n}}=1+2n{{a}_{n}}\)，求数列\(\left\{ {{b}_{n}} \right\}\)的前\(n\)项和\({{T}_{n}}\)．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

(2018•山东) (本小题8分) 如图所示的几何体中，四边形 ABCD是矩形， MA⊥平面 ABCD， NB ⊥平面 ABCD，且 AB=NB=1，AD=MA=2。
(1)求证：NC‖平面 MAD；
(2)求棱锥M-NAD的体积。

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

如图，四边形\(ABCD\)为正方形，\(QA⊥\)平面\(ABCD\)，\(PD\:/\!/QA\)，\(QA=AB= \dfrac {1}{2}PD\)．
\((1)\)证明：\(PQ⊥CQ\)；
\((2)\)求棱锥\(Q-ABCD\)的体积与棱锥\(P-DCQ\)的体积的比值；
\((3)\)求面\(BCQ\)与面\(DCQ\)夹角的余弦值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

已知\(\{{a}_{n}\} \)是公差为\(3\)的等差数列，数列\(\{{b}_{n}\} \)满足\({b}_{1}=1,{b}_{2}= \dfrac{1}{3},{a}_{n}{b}_{n+1}+{b}_{n=1}=n{b}_{n} \)．

\((1)\)求\(\{{a}_{n}\} \)的通项公式； \((2)\)求\(\{{b}_{n}\} \)的前\(n\)项和．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

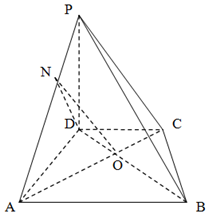在四棱锥\(P-ABCD\)中，\(PD⊥\)底面\(ABCD\)，\(ABCD\)为等腰梯形，且\(AB\:/\!/DC\)，\(AC⊥BD\)，\(AB=2 \sqrt {2}\)，\(DC= \sqrt {2}\)．
\((1)\)若\( \overrightarrow{CM}=λ \overrightarrow{CP}\)，试确定实数\(λ\)的值，使\(PA\:/\!/\)面\(MBD\)；
\((2)\)若\(∠APC=90^{\circ}\)，设\( \overrightarrow{AN}= \dfrac {2}{3} \overrightarrow{AP}\)，求三棱锥\(N-AOD\)的体积．

查看解析收藏纠错相似题

+选题
题型：解答题题类：历年真题难易度：中档

年份：2018

设不等式\(|2x-1| < 1\)的解集为\(M\)，且\(a\)\(\in \)\(M\)，\(b\)\(\in \)\(M.\)
\((1)\)试比较\(ab+1\)与\(a+b\)的大小；

\((2)\)设\(max A\)表示数集\(A\)中的最大数，且\(h=max\)\(\left\{ \dfrac{2}{ \sqrt{a}}, \dfrac{a+b}{ \sqrt{ab}}, \dfrac{2}{ \sqrt{b}}\right\} \)，求\(h\)的取值范围．

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心