题型：填空题 题类：模拟题 难易度：较易
新年份：2021
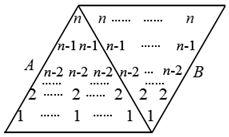“垛积术”在我国古代早期主要用于天文历法，后来用于求高阶等差级数的和．元代数学家朱世杰在沈括\((\)北宋时期数学家\()\)、杨辉\((\)南宋时期数学家\()\)研究成果的基础上，在《四元玉鉴》中利用了“三角垛”求一系列重要的高阶等差级数的和．例如，欲求数列\(1×n\)，\(2×(n-1)\)，\(3×(n-2)\)，…，\((n-1)×2\)，\(n×1\)的和，可设计一个正立的\(n\)行三角数阵，即正三角形\(A\)的区域中所有数的分布规律为：第\(1\)行为\(1\)个\(n\)，第\(2\)行为\(2\)个\(n-1\)，第\(3\)行为\(3\)个\(n-2\)，…，第\(n\)行为\(n\)个\(1\)；再选一个数列\(\{n^{2}\}(\)其前\(n\)项和已知\()\)，可设计一个倒立的\(n\)行三角数阵，即正三角形\(B\)的区域中所有数的分布规律为：第\(1\)行为\(n\)个\(n\)，第\(2\)行为\(n-1\)个\(n-1\)，第\(3\)行为\(n-2\)个\(n-2\)，…，第\(n\)行为\(1\)个\(1.\)这两个三角数阵就组成一个\(n\)行\(n+1\)列的菱形数阵．若已知\(1^{2}+2^{2}+3^{2}+⋯+n^{2}=\dfrac{1}{6}n(n+1)(2n+1)\)，则运用垛积术，求得数列\(1×n\)，\(2×(n-1)\)，\(3×(n-2)\)，…，\((n-1)×2\)，\(n×1\)的和为 ______. 