0-1周期序列在通信技术中有着重要应用.若序列a
1a
2…a
n…满足a
i∈{0,1}(i=1,2,…),且存在正整数m,使得a
i+m=a
i(i=1,2,…)成立,则称其为0-1周期序列,并称满足a
i+m=a
i(i=1,2…)的最小正整数m为这个序列的周期.对于周期为m的0-1序列a
1a
2…a
n…,C(k)=
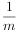
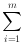
a
ia
i+k(k=1,2,…,m-1)是描述其性质的重
要指标,下列周期为5的0-1序列中,满足C(k)≤
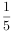
(k=1,2,3,4)的序列是( )
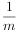
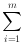 aiai+k(k=1,2,…,m-1)是描述其性质的重
aiai+k(k=1,2,…,m-1)是描述其性质的重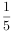 (k=1,2,3,4)的序列是( )
(k=1,2,3,4)的序列是( )