题型:解答题 题类:其他 难易度:较易
年份:2018
已知数列\(\{a_{n}\}\)是等差数列,其前\(n\)项和为\(S_{n}\),数列\(\left\{ \left. b_{n} \right. \right\}\)是公比大于\(0\)的等比数列,且\(b_{1}=-2a_{1}=2\), \(a_{3}+b_{2}=-1\), \(S_{3}+2b_{3}=7\).
\((1)\)求数列\(\{a_{n}\}\)和\(\left\{ \left. b_{n} \right. \right\}\)的通项公式;
\((2)\)令\(c_{n}=\begin{cases} 2,n为奇数 \\ \dfrac{-2a_{n}}{b_{n}},n为偶数 \end{cases}\),求数列\(\left\{ \left. c_{n} \right. \right\}\)的前\(n\)项和\(T_{n}\).
题型:解答题 题类:其他 难易度:较易
年份:2018
如图,\(\triangle ABC\)中,\(∠ACB=90^{\circ} \),\(∠ABC=30^{\circ} \),\(BC= \sqrt{3} \),在三角形内挖去一个半圆\((\)圆心\(O\)在边\(BC\)上,半圆与\(AC\),\(AB\)、分别相切于点\(C\),\(M\),与\(BC\)交于点\(N)\),将\(\triangle ABC\)绕直线\(BC\)旋转一周得到一个旋转体.
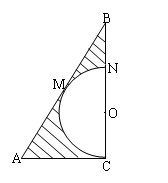
\((1)\)求该几何体中间一个空心球的表面积的大小;
\((2)\)求图中阴影部分绕直线\(BC\)旋转一周所得旋转体的体积.