题型:填空题 题类:期中考试 难易度:较难
年份:2018
\((1)\)已知向量\(\overrightarrow{a} \),\(\overrightarrow{b} \)夹角为\(60^{\circ}\),\(\left| \overrightarrow{a}\right|=2 \),\(\left| \overrightarrow{b}\right|=1 \),则\(\left| \overrightarrow{a}+2 \overrightarrow{b}\right| \)____\(.\)
\((2)\)在等差数列\(\left\{{a}_{n}\right\} \)中,\(a_{1}=7\),公差为\(d\),\(S_{n}\)为其前\(n\)项和,当且仅当\(n=8\)时\(S_{n}\)取得最大值,则\(d\)的取值范围为__________.
\((3)\)已知直三棱柱\(ABC-A_{1}B_{1}C_{1}\)的\(6\)个顶点都在球\(O\)的球面上,若\(AB=3\),\(AC=4\),\(AB⊥AC \),\(AA_{1}=12\),则球\(O\)的表面积为__________.
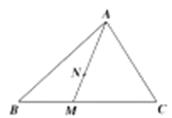
\((4)\)如图,在\(\triangle ABC\)中,\(M\)为\(BC\)上不同于\(B\),\(C\)的任意一点,点\(N\)满足\(\overrightarrow{AN}=2 \overrightarrow{NM} .\)若\(\overrightarrow{AN}=x \overrightarrow{AB}+y \overrightarrow{AC} \),则 \(x^{2}+9y^{2}\)的最小值为_________\(..\)
题型:解答题 题类:期中考试 难易度:较难
年份:2018
在数列\(\left\{ {{a}_{n}} \right\}\)中,\({{a}_{1}}=8\),\({{a}_{4}}=2\),且满足\({{a}_{n+2}}+{{a}_{n}}=2{{a}_{n+1}}\).
\((1)\)求数列\(\left\{ {{a}_{n}} \right\}\)的通项公式; \((2)\)设\({{S}_{n}}\)是数列\(\left\{ \left| {{a}_{n}} \right| \right\}\)的前\(n\)项和,求\({{S}_{n}}\).
题型:填空题 题类:期中考试 难易度:较难
年份:2018
\((1)\)在等差数列\(\{ a_{n}\}\)中,若\(a_{1}{+}a_{7}{+}a_{13}{=}6\),则\(S_{13}{=}\)______ .
\((2)\)函数\(y{=}\log{{ }}_{\frac{1}{2}}(x^{2}{+}2x{-}3)\)的单调递减区间是______ .
\((3)\)在\({\triangle }ABC\)中,\(a{=}\sqrt{3}{,}b{=}1{,}{∠}A{=}\dfrac{\pi}{3}\),则\(\cos B{=}\)______ .
\((4)\)已知点\(A\)是以\(BC\)为直径的圆\(O\)上异于\(B{,}C\)的动点,\(P\)为平面\(ABC\)外一点,且平面\(PBC{⊥}\)平面\({ABC}{,}BC{=}3{,}PB{=}2\sqrt{2}{,}PC{=}\sqrt{5}\),则三棱锥\(P{-}ABC\)外接球的表面积为______ .
题型:选择题 题类:期中考试 难易度:较难
测年份:2018
对于数列\(\left\{ {{a}_{n}} \right\}\),定义\({{A}_{n}}=\dfrac{{{a}_{1}}+2{{a}_{2}}+\cdots +{{2}^{n-1}}{{a}_{n}}}{n}\)为数列\(\left\{ {{a}_{n}} \right\}\)的“好数”\(.\)已知某数列\(\left\{ {{a}_{n}} \right\}\)的“好数”\({{A}_{n}}={{2}^{n+1}}\),记数列\(\left\{ {{a}_{n}}-kn \right\}\)的前\(n\)项和为\({{S}_{n}}\),若\({{S}_{n}}\leqslant {{S}_{6}}\)对任意的\(n\in {{N}^{*}}\)恒成立,则实数\(k\)的取值范围为( )